|
El problema de la minimización del gasto 2.- Demanda compensada y función de gasto |
En la página anterior hemos buscado la forma más barata de alcanzar cierta utilidad dados unos precios. Una vez analizado ese problema nos planteamos el siguiente paso: ¿podemos resolver el problema de forma general, sin usar un nivel de utilidad y unos precios concretos?
La respuesta a esta pregunta no es especialmente complicada, pero puede resultar algo abstracta. Por eso, antes de expresarla en términos generales conviene que trabajes los siguientes ejemplos.
John MaryEl problema de minimización del gasto con unos datos genéricos no es distinto de los que hemos resuelto anteriormente para datos concretos. Se trata de buscar el punto más barato de la curva de indiferencia, y eso pasará donde una recta isocoste es tangente a la curva. Por tanto el punto que buscamos ha de cumplir la ecuación de la curva de indiferencia, y también la condición de tangencia. Esta afirma que en un punto de tangencia la pendiente de la curva ($\mathrm{RMS}$) ha de ser igual a la pendiente de la recta isocoste (el cociente de precios, $-\frac{p_C}{p_N}$ ).
Podemos plantear el sistema con las dos ecuaciones: \[ \left. \begin{array}{c} \mathrm{U}(x_1, x_2) = u \\ \mathrm{RMS}(x_1, x_2) =-\frac{p_1}{p_2} \end{array} \right\} \]
La novedad es que cuando planteemos este sistema para un consumidor con una función de utilidad concreta (y su correspondiente relación marginal de sustitución), tendremos un sistema en el que habrá dos ecuaciones y cinco letras (variables): $x_1$, $x_2$, $p_1$, $p_2$ y $u$.
Debe quedar claro que las incógnitas a resolver son $x_1$ y $x_2$, mientras que $p_1$, $p_2$ y $u$ son los parámetros; aunque no tengan un valor concreto son los datos del problema.
Resolver este sistema es despejar en él $x_1$ y $x_2$, de forma que queden como funciones de los parámetros.
Llamamos funciones de demanda compensada (o de demanda hicksiana) a las funciones que calculan las cantidades de los bienes 1 y 2 que permiten alcanzar la utilidad $u$ con el mínimo gasto posible cuando los precios son $p_1$ y $p_2$.
\[ x_1^h = h_1(p_1, p_2, u) \quad \quad x_2^h = h_2(p_1, p_2, u) \] El siguiente paso será hacernos algunas preguntas sobre estas funciones de demanda compensada (entre otras el por qué de su nombre), pero antes veremos un par de ejemplos más.
El primero es otro caso de preferencias Cobb-Douglas, un poco más trabajoso que el de John pero sin más dificultad que tener cuidado al operar.* Es el momento de usar lápiz y papel y aprender haciendo, no sólo mirando.
En el segundo ejemplo volveremos a encontrarnos con Sandra, y habrá que pensar un poco más porque la tangencia puede no funcionar (como pasó ya anteriormente).
Ejemplo SandraPara contestar la pregunta la redirigimos hacia el inicio del problema. ¿Qué ocurre en el problema del consumidor si, por ejemplo, sube el precio del bien 1?
El problema de minimización consiste en elegir el punto más barato de la curva de indiferencia $u$. La curva de indiferencia no depende para nada de los precios, así que cuando un precio cambia el conjunto de alternativas no varía. Sigue siendo exactamente el mismo, formado por las cestas que cumplen la ecuación de la curva \[ \mathrm{U}(x_1, x_2) = u \]
La variación del precio sí cambiará el valor a precios de mercado de las combinaciones de bienes. Un aumento de $p_1$ aumenta la pendiente de las rectas isocoste y, por tanto, se modifica la ecuación correspondiente a la condición de tangencia.* Recuerda que la $\mathrm{RMS}(x_1, x_2)$ es la pendiente de la curva de indiferencia. Puesto que la curva sigue siendo la misma, su pendiente no varía al cambiar el precio. \[ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \]
¿Podemos ahora decir algo sobre la respuesta de la demanda compensada del bien 1 (y de la del bien 2) a la subida del precio del bien 1? Observa la figura.
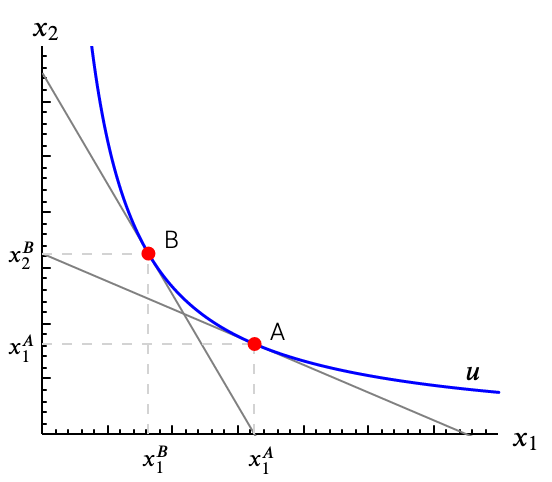
¿Puedes saber qué ha pasado con los precios? ¿Cuál ha cambiado, y en qué sentido (subir o bajar)? Sol.
Podemos concluir que la respuesta de la demanda compensada de un bien a una subida de su precio siempre será reducir el consumo de ese bien, y aumentar el del otro. El único requisito es que las curvas de indiferencia sean convexas (que se cumpla la propiedad de la relación marginal de sustitución decreciente).* Hemos visto el caso de Mary, en que las demandas no cambian al variar el precio. Es un caso en que la $\mathrm{RMS}$ no es decreciente.
La afirmación anterior puede expresarse formalmente mediante los signos de las derivadas parciales de las funciones de demanda compensada. Podemos afirmar que \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} < 0 \quad \quad \frac{\partial h_1(p_1, p_2, u)}{\partial p_2} > 0 \] \[ \frac{\partial h_2(p_1, p_2, u)}{\partial p_1} > 0 \quad \quad \frac{\partial h_2(p_1, p_2, u)}{\partial p_2} < 0 \]
Ejemplo
Comprobemos los signos de las derivadas parciales de las funciones de demanda hicksiana calculadas anteriormente para la función de utilidad $\mathrm{U}(x_1, x_2) = x_1^2 x_2^3$ \[ h_1(p_1, p_2, u) = \left( \frac{2 p_2}{3 p_1}\right)^{3/5} u^{1/5} \quad \quad h_2(p_1, p_2, u) = \left( \frac{3 p_1}{2 p_2}\right)^{2/5} u^{1/5}\] Podemos afirmar que \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} = \left( \frac{2 p_2}{3}\right)^{3/5} u^{1/5} \left( -\frac{3}{5}\right) p_1^{-8/5} < 0 \] ya que al derivar obtenemos un producto de cuatro factores en el que tres de ellos son positivos y uno es negativo, por lo que el resultado es negativo (para cualquier valor de $p_1$, $p_2$ y $u$).
Al derivar $h_1$ respecto de $p_2$ obtenemos un valor positivo \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_2 } = \left( \frac{2}{3 p_1}\right)^{3/5} u^{1/5} \left( \frac{3}{5}\right) p_2^{-2/5} > 0 \]
(un producto de cuatro factores positivos.)
Puedes comprobar de la misma manera los signos de las derivadas parciales de $h_2(p_1, p_2, u)$.
Quizá las figuras de más arriba te hayan resultado familiares. La siguiente figura muestra a la izquierda la respuesta de la demanda compensada a una subida de $p_1$, tal como estamos viendo. La figura de la derecha es conocida: el Efecto Total de una subida del precio (cuando maximizábamos la utilidad dada una renta) y su descomposición en Efecto Sustitución y Efecto Renta.
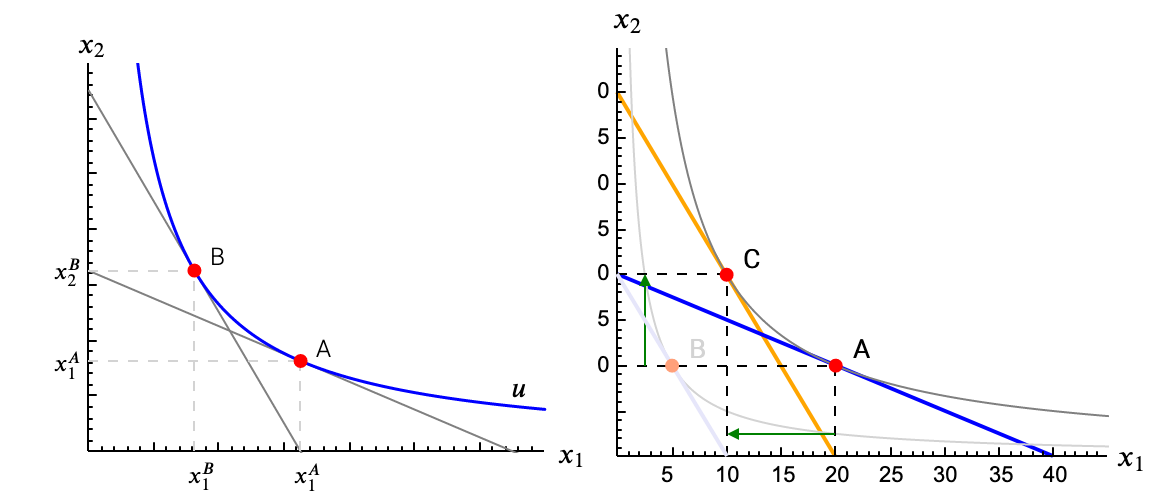
Vemos que la respuesta de la demanda compensada en la figura de la izquierda coincide con parte de la figura de la derecha, concretamente con el efecto sustitución.
Llamábamos Efecto Sustitución a la respuesta del consumidor a una variación del precio cuando al mismo tiempo compensábamos la renta para mantener constante el poder adquisitivo. Y la respuesta de la demanda compensada es por definición la que mantiene constante la utilidad, al mínimo coste (con la mínima necesidad de renta). En realidad en ambos casos estamos haciendo lo mismo. Podemos afirmar que la variación de la demanda compensada es igual al Efecto Sustitución. De hecho, el nombre de demanda compensada hace referencia a esto, pues es la demanda del consumidor suponiendo que tenga la renta necesaria para mantener constante la utilidad.
La idea de asociar mantenimiento del poder adquisitivo con mantenimiento del nivel de utilidad fue propuesta por el economista John Hicks. Por eso a la demanda compensada se le llama también demanda hicksiana, y usamos la inicial de su apellido para las funciones en la notación matemática.
La función de demanda compensada del bien 1 Todo lo que vamos a ir diciendo para la demanda de bien 1 puede trasladarse a la demanda del bien 2, sin más que cambiar los subíndices. es una función que depende de tres variables $p_1$, $p_2$ y $u$. Si fijamos los valores de $p_2$ y $u$ la función se convierte en una relación entre el precio del bien 1 y la cantidad demandada. \[ h_1(p_1, \bar{p}_2, \bar{u}) = h_1(p_1) \]
Esta relación la podemos representar gráficamente como una curva, a la que llamaremos curva de demanda compensada del bien 1.* Seguramente ya has notado que es lo mismo que hicimos a partir de la función de demanda individual, cuando fijando $p_2$ y $m$ obteníamos la curva de demanda del bien 1, o fijando $p_1$ y $p_2$ obteníamos la curva de Engel.
Ejemplo
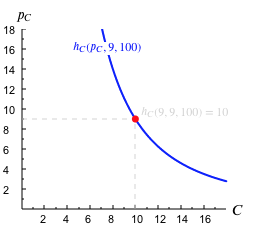
Hemos calculado anteriormente la función de demanda de caramelos de John, que resultaba ser \[ h_C(p_C, p_N, u) = \sqrt{\frac{p_N}{p_C} u} \]
¿Cuál será la correspondiente curva de demanda compensada de caramelos si $p_N=9$ y $u=100$? Sol.
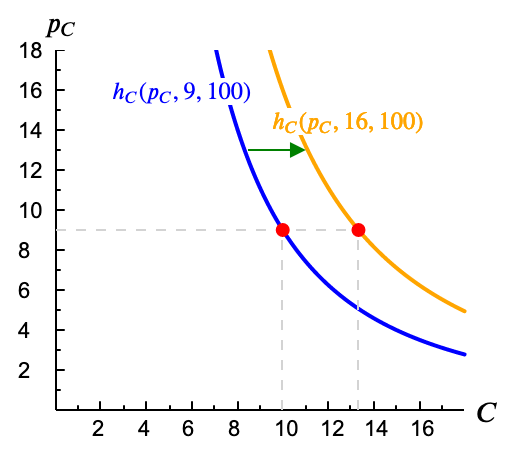
¿Qué ocurriría en la figura si cambiase $p_2$? Hemos visto anteriormente que, dado un $p_1$ fijo, una subida de $p_2$ aumentaría la demanda del bien 1.* La subida de $p_2$ reduce la pendiente de las isocoste y eso lleva a bajar por la curva de indiferencia, aumentando el $x_1$ demandado. Como esto es cierto para cualquier valor de $p_1$, podemos decir que la demanda compensada cumple que \[ p_2' > p_2 \quad \Longrightarrow \quad h_1(p_1, p_2', u) > h_1(p_1, p_2, u) \quad \forall p_1 \]
La expresión anterior significa que una subida de $p_2$ da lugar a una nueva curva de demanda compensada del bien 1 que estará más a la derecha que la inicial (suele decirse, de manera más gráfica, que la subida de $p_2$ desplaza la curva de demanda compensada del bien 1 hacia la derecha).
Ejemplo
Exactamente igual que hemos definido la curva de demanda compensada del bien 1 podemos hablar de la curva de demanda compensada del bien 2. El siguiente ejemplo/ejercicio te pide que calcules la curva de demanda compensada del bien 2 para las preferencias de un ejemplo anterior.
Ejemplo
Hemos calculado ya las funciones de demanda de las preferencias dadas por \[ \mathrm{U}(x_1, x_2) = x_1^2 x_2^3 \]
Calcula y representa (estaría bien que hagas el ejercicio a mano) la curva de demanda del bien 2 para $u=32$ y $p_1=1$. Después obtén la curva para un nuevo precio $p_1'=\frac{2}{3}$. ¿Estará la nueva curva más a la derecha o más a la izquierda que la inicial? (deberías saber la respuesta a esta pregunta ya antes de hacer los cálculos). \[ h_1(p_1, p_2, u) = \left( \frac{2 p_2}{3 p_1}\right)^{3/5} u^{1/5} \quad \quad h_2(p_1, p_2, u) = \left( \frac{3 p_1}{2 p_2}\right)^{2/5} u^{1/5}\]
Sol.Usamos los valores de $u$ y $p_1$ en la función $h_2(\cdot)$. \[ h_2(1, p_2, 32) = \left( \frac{3 }{2 p_2}\right)^{2/5} 32^{1/5} = \left( \frac{2}{3}\right)^{2/5} 2 \frac{1}{p^{2/5}} \simeq \frac{2.35}{p_2^{2/5}}\] \[ h_2(\frac{2}{3}, p_2, 32) = \left( \frac{3 \frac{2}{3} }{2 p_2}\right)^{2/5} 32^{1/5} = \frac{2}{p_2^{2/5}}\]
Comparando las dos funciones, para cualquier $p_2$ la primera función demanda más que la segunda. Por tanto al bajar $p_1$ la curva de demanda compensada de bien 2 se desplaza hacia la izquierda.
Todas las curvas de demanda compensada que hemos visto dibujadas tienen pendiente negativa. ¿Será esto así siempre? Eso es lo que afirma la llamada ley de la demanda compensada: Todas las curvas de demanda compensada tienen pendiente negativa; a mayor precio menor cantidad demandada.
En realidad ya hemos afirmado esto mismo más arriba, con otras palabras. Dijimos que un aumento del cociente de precios que es lo que pasa al aumentar $p_1$, llevaba a que la cesta demandada se mueva por la curva de indiferencia reduciendo el consumo de bien 1 y aumentando el de bien 2.
También lo hemos usado para justificar el sentido del desplazamiento de la curva de demanda de un bien cuando cambia el precio del otro.
Hay un par de observaciones adicionales que conviene hacer.
Un enunciado más cuidadoso de la ley de la demanda compensada debería decir que las curvas de demanda compensada nunca tendrán pendiente positiva (fíjate que así cabe la posibilidad de la no respuesta, como en el caso de Mary).
La siguiente demostración prueba la ley de la demanda compensada como la acabamos de enunciar, y lo hace además sin necesidad de suponer convexidad para las preferencias. Aunque se presenta dentro de 'Ver Mates' no necesita instrumental matemático especial (aunque sí un poco de cuidado).
Por definición, las demandas compensadas nos dan la cesta que a unos precios dados consigue la utilidad $u$ con el menor gasto posible. Por tanto el valor monetario de la cesta demandada es menor (o en todo caso igual) que el de cualquier otro punto de la curva $u$ para esos mismos precios.
Vamos a suponer unos datos iniciales, $p_1$, $p_2$ y $u$, y un cambio en el precio del bien 1 a $p_1'$ (el nuevo precio del bien 1 puede ser mayor o menor que el inicial).
Dado que $p_2$ y $u$ van a permanecer constantes todo el tiempo, para facilitar la lectura escribiremos $h_1(p_1)$ y $h_2(p_1)$ en lugar de $h_1(p_1, p_2, u)$ y $h_2(p_1, p_2, u)$.
Inicialmente se demanda la cesta $\big( h_1(p_1), h_2(p_1) \big)$, y tras el cambio la cesta óptima es $\big( h_1(p_1'), h_2(p_1') \big)$. Ambos puntos están en la curva $u$.
Cuando a los precios iniciales se elegía el primer punto, debía ser porque a esos precios ningún otro costaba menos que él. Y uno de esos otros es el $\big( h_1(p_1'), h_2(p_1') \big)$. Por tanto podemos escribir que \[ p_1 h_1(p_1) + p_2 h_2(p_1) \leq p_1 h_1(p_1') + p_2 h_2(p_1') \]
Razonando de la misma forma, debe ser cierto que a los nuevos precios el segundo punto cuesta menos que el primero ($p_2$ es el mismo; sólo cambia $p_1$) \[ p_1' h_1(p_1') + p_2 h_2(p_1') \leq p_1' h_1(p_1) + p_2 h_2(p_1) \]
Si sumamos las dos desigualdades tenemos
$p_1 h_1(p_1) + p_2 h_2(p_1) + p_1' h_1(p_1') + p_2 h_2(p_1') $ $\quad \quad \leq p_1 h_1(p_1') + p_2 h_2(p_1') + p_1' h_1(p_1) + p_2 h_2(p_1) $
El segundo sumando del lado izquierdo es igual al cuarto sumando del lado derecho, y el cuarto del lado izquierdo igual al segundo del lado derecho. Así la expresión se simplifica a \[ p_1 h_1(p_1) + p_1' h_1(p_1') \leq p_1 h_1(p_1') + p_1' h_1(p_1) \]
Pasamos todos los sumandos al lado izquierdo y agrupamos para los precios \[ p_1' [h_1(p_1')-h_1(p_1) ] + p_1 [h_1(p_1) - h_1(p_1')] \leq 0 \]
Podemos cambiar el signo del segundo sumando al mismo tiempo que los signos dentro del segundo paréntesis \[ p_1' [h_1(p_1')-h_1(p_1) ] - p_1 [h_1(p_1') - h_1(p_1)] \leq 0 \]
Y finalmente tenemos \[ (p_1' - p_1)\cdot [h_1(p_1')-h_1(p_1) ] \leq 0 \]Ahora ya podemos afirmar que si sube el precio del bien 1 ($p_1' > p_1$), para que se cumpla la desigualdad anterior ha de ser cierto que $h_1(p_1') - h_1(p_1)\leq 0 $. Esto es, al subir $p_1$ la cantidad demandada baja (o en todo caso no varía). No es posible que al subir el precio la cantidad demandada aumente. Por tanto hemos demostrado lo que afirma la ley.
Ya hemos visto que la respuesta de la demanda compensada no depende de lo que pasa con uno u otro precio, sino con la pendiente de las isocoste, esto es, el cociente de precios.
Cualquier variación de precios que aumente la pendiente de las isocoste llevará a demandar menos bien 1 y más bien 2 (y viceversa).
Ejemplo
El último caso aporta una novedad respecto a los otros, ¿cuál? Sol.Si los precios cambian pero la pendiente de las isocostes no varía la cesta demandada sigue siendo la misma. ¿Cuándo ocurre eso? Sol.
Una variación simultánea de los dos precios en la misma proporción no modifica la pendiente de las rectas isocoste. El nuevo punto de tangencia será el mismo que el inicial, ya que en realidad el sistema de ecuaciones no ha variado.
Ejemplo
¿Cómo cambia la demanda si los precios suben simultáneamente un 50%?Sol.
Aplicamos de nuevo las funciones de demanda usando los nuevos precio \[ h_C(6, 13.5, 100) = \sqrt{\frac{13.5}{6} 100} = 15 \] \[ h_N(6, 13.5, 100) = \sqrt{\frac{6}{13.5} 100} = \frac{20}{3} \]
La cesta demandada sigue siendo la misma.
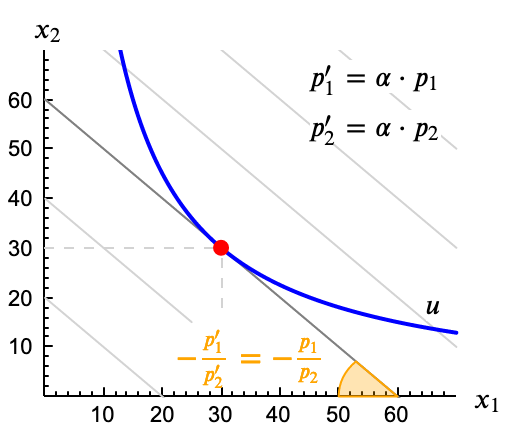
Podemos afirmar que las demandas condicionadas son funciones homogeneas de grado 0 en los precios de los bienes, \[ \forall \alpha > 0, \forall (p_1, p_2), \quad h_1(\alpha p_1, \alpha p_2, u) = h_1(p_1, p_2, u) \]
Para demostrar la afirmación planteamos el problema de minimización para los nuevos precios, $p_1' = \alpha p_1$ y $p_2' = \alpha p_2$
La solución inicial se obtiene resolviendo el sistema \[ \left. \begin{array}{c} \mathrm{U}(x_1, x_2) \\ \mathrm{RMS}(x_1, x_2) =-\frac{p_1}{p_2} \end{array} \right\} \]
Para los nuevos precios el sistema es \[ \left. \begin{array}{c} \mathrm{U}(x_1, x_2) \\ \mathrm{RMS}(x_1, x_2) =-\frac{p_1'}{p_2'} \end{array} \right\} \]
Como \[ -\frac{p_1'}{p_2'} = -\frac{\alpha p_1}{\alpha p_2} = -\frac{p_1}{p_2} \]
los dos sistemas son equivalentes, por lo que tienen la misma solución. Al variar los dos precios en igual proporción el valor de las funciones de demanda compensada permanece constante.
Ejemplo
¿Y si tomamos las funciones de demanda compensada de Sandra, que eran algo más complejas? \[ h_1(p_1, p_2, u) = \left\{ \begin{array}{ccc} \frac{25}{4} \left( \frac{p_1}{p_2}\right)^2 & \mathrm{if} & u > \frac{25 p_2}{2 p_1} \\ \\ \frac{u^2}{25} & \mathrm{if} & u \leq \frac{25 p_2}{2 p_1} \end{array} \right. \] \[ h_2(p_1, p_2, u) = \left\{ \begin{array}{ccc} u - \frac{25}{2} & \mathrm{if} & u > \frac{25 p_2}{2 p_1} \\ \\ 0 & \mathrm{if} & u \leq \frac{25 p_2}{2 p_1} \end{array} \right. \]
¿Serán también homogéneas de grado 0 en los precios? (lo comprobamos para el bien 1) \[ h_1(\alpha p_1, \alpha p_2, u) = \left\{ \begin{array}{ccc} \frac{25}{4} \left( \frac{\alpha p_1}{\alpha p_2}\right)^2 & \mathrm{if} & u > \frac{25 \alpha p_2}{2 \alpha p_1} \\ \\ \frac{u^2}{25} & \mathrm{if} & u \leq \frac{25 \alpha p_2}{2 \alpha p_1} \end{array} \right. \]
Podemos ver que $\alpha$ desaparece al simplificar en los cocientes, tanto en la propia función como en la condición que define los tramos. De manera que, efectivamente, $ h_1(\alpha p_1, \alpha p_2, u) = h_1( p_1, p_2, u) $
La homogeneidad de grado 0 en precios de las funciones de demanda compensada es una propiedad general, que no depende del tipo de preferencias. Esto es así porque el cambio proporcional de los precios no afecta ni al conjunto de alternativas, que viene dado por la curva de indiferencia, ni a la condición de tangencia, ya que el valor del cociente de precios no varía.
Una vez calculada la cesta demandada (o las funciones de demanda) hay una pregunta que surge de forma natural.* De hecho, en los ejemplos de la página anterior ya la fuimos planteando.
¿Y eso cuánto dinero va a costar?
Si recordamos el ejemplo del abuelo y los nietos, que abría el capítulo, cada uno calculará qué combinación de caramelos y nubes le conviene más, pero el abuelo querrá saber cuánto dinero necesitan.
En los ejemplos con datos concretos bastaba con usar los precios para calcular el valor de mercado de la cesta elegida. Ahora la idea será la misma, aunque trabajando con funciones.
Llamamos función de gasto de un consumidor a la función que calcula la mínima cantidad de dinero necesaria para alcanzar un nivel de utilidad $u$ cuando los precios son $p_1$ y $p_2$.
Para obtener la función de gasto sólo tenemos que calcular el coste de la cesta más barata, esto es, de la cesta formada por las demandas compensadas. \[ e(p_1, p_2, u) = p_1 \cdot h_1(p_1, p_2, u) + p_2 \cdot h_2(p_1, p_2, u) \]
John
¿Cuál será la función de gasto de John?
Sus funciones de demanda compensada son \[ h_C(p_C, p_N, u) = \sqrt{\frac{p_N}{p_C} u} \quad h_N(p_C, p_N, u) = \sqrt{\frac{p_C}{p_N} u} \]
Calculamos la función de gasto: \[ e(p_C, p_N , u) = p_C \cdot \sqrt{\frac{p_N}{p_C} u} + p_N \cdot \sqrt{\frac{p_C}{p_N} u} = \sqrt{p_C p_N u} + \sqrt{p_N p_C u} = 2 \sqrt{p_C p_N u} \]
¿Puedes calcular la función de gasto de Mary? (recuerda que sus funciones de demanda compensada eran muy sencillas, $h_C(p_C, p_N, u) =u $ y $h_N(p_C, p_N, u) =u $) Sol.
El siguiente ejemplo resulta algo más matemático, pero sólo porque requiere operar con exponentes fraccionarios.
Ejemplo
¿Cuál será lal función de gasto correspondiente a la función de utilidad $\mathrm{U}(x_1, x_2) = x_1^2 x_2^3$ ? Tenemos las funciones de demanda compensada \[ h_1(p_1, p_2, u) = \left( \frac{2 p_2}{3 p_1}\right)^{3/5} u^{1/5} \quad \quad h_2(p_1, p_2, u) = \left( \frac{3 p_1}{2 p_2}\right)^{2/5} u^{1/5}\]
Sol.Es posible establecer algunas propiedades de la función de gasto, simplemente razonando a partir de su definición.
Para justificar esta afirmación lo más fácil es razonar gráficamente.
Dada una utilidad $u_0$, la función de gasto calcula el valor a precios de mercado del punto más barato de la curva de indiferencia $u_0$. Llamaremos $e_0$ al gasto correspondiente a ese punto.
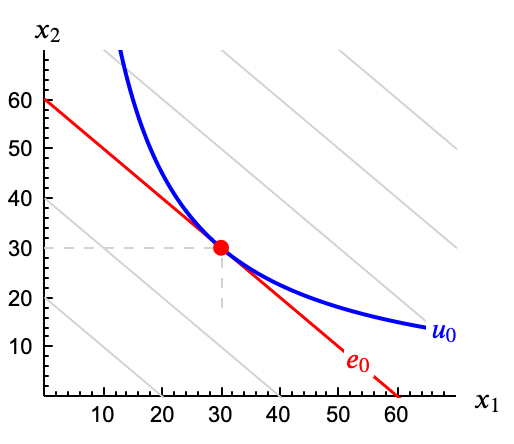
Todos los puntos que cuesten menos que $e_0$ están por debajo de la isocoste $e_0$. Todos los puntos con utilidad mayor que $u_0$ están por encima de la curva de indiferencia $u_0$. Si queremos aumentar al utilidad forzosamente tendremos que ir a un punto que cuesta más que $e_0$. Por tanto no es posible una función de gasto decreciente en la utilidad.
Formalmente expresaríamos la propiedad usando el signo de la derivada parcial de la función de gasto respecto de $u$, \[ \frac{\partial e(p_1, p_2, u)}{\partial u} > 0 \]
Una subida en el precio de un bien siempre hará que aumente el gasto necesario para mantener la utilidad inicial.* Puede haber alguna excepción en el caso de soluciones de esquina, pero en esos casos el gasto podría permanecer constante, nunca descender.
A primera vista puede surgir la duda de si responder a la subida del precio de un bien con una reducción de su consumo (y un aumento del consumo del otro) podría esquivar el impacto de la subida del precio. La figura nos permitirá ver que no es así.
Supongamos que aumenta $p_1$. Pulsa el botón 1.
Podemos concluir que al moverse a otro punto de la curva el consumidor consigue amortiguar algo el impacto de la subida del precio. El nuevo punto demandado cuesta menos que lo que cuesta ahora el punto inicial, pero cuesta más que lo que costaba antes el punto inicial. Al aumentar $p_1$ el valor de la función de gasto aumenta.
Una vez más podemos recoger la propiedad usando las derivadas parciales \[ \frac{\partial e(p_1, p_2, u)}{\partial p_i} > 0 \quad \forall i \in \{ 1, 2\} \]
Queda como ejercicio razonar que la propiedad es la misma para $p_2$* El razonamiento es el mismo, aunque habrá que modificar la figura para recoger, con la misma lógica, lo que pasa al subir $p_2$.
Una última cuestión. ¿Se cumplirá la propiedad en el caso de Mary (en el que no se cumple la condición de tangencia)? Sol.
Para justificar esta propiedad basta recordar que hemos visto que ante un cambio proporcional en los dos precios la cesta demandada sigue siendo la misma. El gasto de comprar el mismo punto aumentará en la misma proporción que los precios (si los precios se multiplican por 2, comprar lo mismo costará el doble).
Lo que acabamos de ver significa que la función de gasto es homogénea de grado 1 en los precios de los bienes. If $p_1'= \alpha p_1$ y $p_2'= \alpha p_2$, \[ \forall \alpha >0 \quad e(\alpha p_1, \alpha p_2, u) = \alpha \cdot e(p_1, p_2, u) \]
Para demostrarlo usamos la definición de la función de gasto \[ e(p_1', p_2', u) = p_1' \cdot h_1(p_1', p_2', u) + p_2' \cdot h_2(p_1', p_2', u) \] \[ e(\alpha p_1, \alpha p_2, u) = \alpha p_1 \cdot h_1(\alpha p_1, \alpha p_2, u) + \alpha p_2 \cdot h_2(\alpha p_1, \alpha p_2, u) \]
Pero las funciones de demanda compensada son homogéneas de grado 0 en los precios, por lo que podemos escribir \[ e(\alpha p_1, \alpha p_2, u) = \alpha p_1 \cdot h_1(p_1, p_2, u) + \alpha p_2 \cdot h_2(p_1, p_2, u) \] Y agrupando factores,
$e(\alpha p_1, \alpha p_2, u) = \alpha \cdot \left[p_1 \cdot h_1(p_1, p_2, u) + p_2 \cdot h_2(p_1, p_2, u) \right] $ $\quad = \alpha \cdot e( p_1, p_2, u)$
El ejemplo te pide que compruebes la propiedad para las funciones de gasto obtenidas en ejemplos anteriores.
Ejemplo
Comprueba en cada caso la homogeneidad de grado 1 en los precios.
La última propiedad se conoce como el Lemma de Shephard, y afirma que las demandas compensadas de los bienes pueden obtenerse como las derivadas parciales de la función de gasto respecto de los precios. \[ \frac{\partial e( p_1, p_2, u) }{\partial p_1} = h_1(p_1, p_2, u) \quad \quad \frac{\partial e( p_1, p_2, u) }{\partial p_2} = h_2(p_1, p_2, u) \]
Para demostrar el Lemma partimos de la definición de la función de gasto y hacemos la derivada parcial respecto de $p_1$* Los pasos para el bien 2 serían idénticos. Sería un buen ejercicio replicar el razonamiento, por escrito. \[ e( p_1, p_2, u) = p_1 \cdot h_1(p_1, p_2, u) + p_2 \cdot h_2(p_1, p_2, u) \] \[ \frac{\partial e( p_1, p_2, u) }{\partial p_1} = h_1(p_1, p_2, u) + p_1 \frac{\partial h_1(p_1, p_2, u) }{\partial p_1} + p_2 \frac{\partial h_2(p_1, p_2, u) }{\partial p_1}\]
Pero las demandas compensadas vienen de resolver el problema de la minimización del gasto, por lo que han de cumplir sus condiciones de primer orden. Concretamente, en el óptimo debe ser cierto que \[ p_1 = \mu \cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} \quad \quad p_2 = \mu \cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \]
Sustituyendo los precios en la expresión anterior tenemos \[ \frac{\partial e( \cdot) }{\partial p_1} = h_1( \cdot) + \mu \cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} \cdot \frac{\partial h_1( \cdot) }{\partial p_1} + \mu \cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \cdot \frac{\partial h_2( \cdot) }{\partial p_1}\] \[ \frac{\partial e( \cdot) }{\partial p_1} = h_1( \cdot) + \mu \cdot \left[ \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} \cdot \frac{\partial h_1( \cdot) }{\partial p_1} + \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \cdot \frac{\partial h_2( \cdot) }{\partial p_1} \right]\]
Por otra parte, puesto que elegimos la demanda compensada entre los puntos que tienen utilidad $u$, debe cumplirse que \[ \mathrm{U}(h_1( \cdot), h_2( \cdot)) = u \]
Y derivando la expresión respecto de $p_1$\[ \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} \cdot \frac{\partial h_1( \cdot) }{\partial p_1} + \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \cdot \frac{\partial h_2( \cdot) }{\partial p_1} = 0 \]
Pero esta es la expresión entre corchetes en la ecuación anterior, de manera que, como queríamos demostrar, \[ \frac{\partial e( p_1, p_2, u) }{\partial p_1} = h_1(p_1, p_2, u) \]
Ejemplo
Si no lo recuerdas puedes comprobar que los valores obtenidos corresponden a las demandas compensadas de Mary.
Los valores de las derivadas coinciden con las demandas compensadas que obtuvimos para John.
Puedes comprobar que $\left( \frac{2}{3}\right)^{3/5} = $0.784, por lo que efectivamente se comprueba el Lemma para el bien 1. Queda como ejercicio la comprobación para el bien 2.
El Lemma de Shephard tiene una lectura adicional que nos será útil en breve.
La derivada de la función de gasto respecto del precio de un bien puede interpretarse como "lo que varía el gasto necesario para alcanzar la utilidad $u$ por unidad monetaria de subida del precio de un bien".
Si, como afirma el Lemma,
\[ \frac{\partial e( p_1, p_2, u) }{\partial p_1} = h_1(p_1, p_2, u) \]significa que cuando el precio del bien 1 suba un euro, el gasto necesario para mantener constante la utilidad aumentará en $h_1(\cdot)$ unidades monetarias, esto es, en tantos euros como unidades del bien 1 se estaban demandando. * Esta afirmación es cierta en términos de derivadas, esto es, para una variación del precio muy pequeña. En su momento vimos que cuando la variación no es tan pequeña la compensación necesaria para mantener constante la utilidad es algo menor.
Funciones de demanda compensada Curva de demanda compensada Ley de la demanda compensada Función de gasto Lemma de Shephard