Sandra es una consumidora cuyas preferencias pueden representarse por la función
\[ \mathrm{U}(x_1, x_2) = 5\cdot \sqrt{x_1} + x_2 \]
El objetivo es calcular las funciones de demanda de Sandra para ambos bienes, pero vayamos poco a poco.
¿Qué cesta demandará Sandra si tiene una renta $m=55$ y los precios son $p_1=1$ y $p_2=2$?
Las utilidades marginales son
Cada utilidad marginal de cada bien es la derivada parcial de la función de utilidad respecto del bien
\[ \mathrm{UMg}_1(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} = \frac{5}{2 \sqrt{x_1}} \] \[ \mathrm{UMg}_2(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} = 1 \]Podemos calcular la relación marginal de sustitución con el cociente de las utilidades marginales: \[ \mathrm{RMS}(x_1, x_2) = -\frac{ \mathrm{UMg}_1(x_1, x_2)}{ \mathrm{UMg}_2(x_1, x_2)} = - \frac{5}{2 \sqrt{x_1}} \]
El siguiente paso es plantear el sistema formado por la ecuación presupuestaria y la condición de tangencia: \[ \left. \begin{array}{c} p_1 x_1+ p_2 x_2 = m \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \end{array} \right\} \quad \Longrightarrow \quad \left. \begin{array}{c} x_1 + 2\cdot x_2 = 55 \\ - \frac{5}{2 \sqrt{x_1}} = -\frac{1}{2} \end{array} \right\} \]
Resuelve el sistema. ¿Algún comentario?Sol.
Tenemos que con estos datos la decisión de Sandra sería comprar la cesta $(x_1^*, x_2^*) = (25, 15) $ .
¿Y si con los mismos precios la renta fuera $m' = 15$? (Resuelve, y si encuentras algo raro piensa un poco antes de mirar la solución)Sol.
Pero ahora, al llevar ese 25 a la otra ecuación resulta que
\[ x_1 + 2 x_2 = 15 \Longrightarrow 25+2x_2= 15 \Longrightarrow x_2=-5\]Pero una cantidad negativa de un bien no es una solución aceptable (no sabemos qué puede significar un consumo negativo). ¿Qué ha pasado aquí?
Quizá no te haya hecho falta mirar la solución para darte cuenta de que $x_1^*=25$ era una solución imposible, pues la renta $m=15$ no llega para pagarla. ¿Hemos hecho entonces algo mal? Matemáticamente no, pero la figura nos ayudará a entender lo que ha ocurrido.
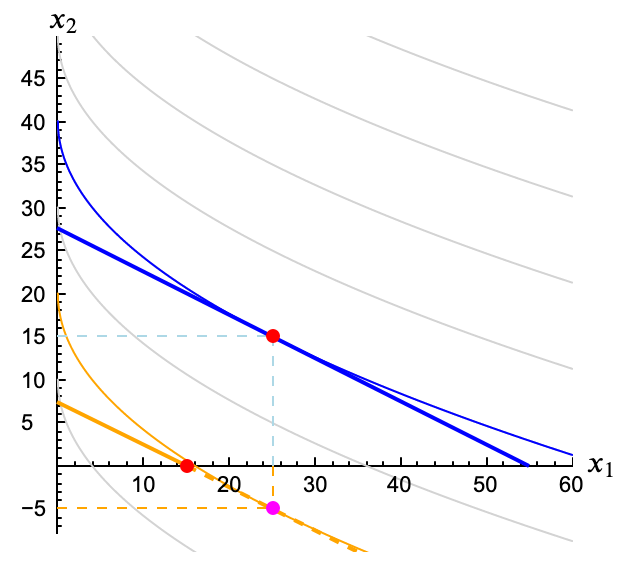
Las curvas de nivel de la función de utilidad de Sandra cortan el eje horizontal. En términos matemáticos esto no tiene nada de raro, pero en términos económicos los valores negativos de $x_1$ o $x_2$ no tienen sentido. Sólo entenderíamos como curvas de indiferencia la parte de las curvas de la zona positiva.
Para la recta de balance inicial, la azul, el punto óptimo viene dado por la tangencia, como esperábamos. Pero en el segundo caso, en la recta de balance naranja, la tangencia nos llevaría a un punto por debajo del eje horizontal (y los puntos de la parte discontinua de la recta naranja no son aceptables). ¿Significa eso que con estos datos el problema no tiene solución? Sol.
Resumiendo, dados estos precios Sandra quiere compran 25 unidades de bien 1, que cuestan 25 libras. Si le sobra dinero lo gasta en bien 2. Si no le llega para comprar las 25 unidades de bien 1 compra todo lo que puede con su renta (y por tanto nada de bien 2).
¿Qué habría pasado con otros precios, por ejemplo $p_1=5$ y $p_2=6$ ? Sol.