|
El problema de la minimización del gasto 3.- La ecuación de Slutsky |
Las herramientas adquiridas a partir de la minimización del gasto permiten expresar de una forma diferente, más formal, la descomposición del Efecto Total de la variación de un precio en los Efectos Sustitución y Renta.
La llamada ecuación de Slutsky expresa los efectos en términos de derivadas parciales, por lo que buena parte de esta página está destinada a quienes siguen el texto incluyendo las partes más matemáticas. Sería posible saltar a la siguiente y seguir adelante con el curso. Pero no es raro encontrar referencias a la ecuación de Slutsky en la literatura económica, por lo que puede merecer la pena dedicarle un poco de atención. Así, antes de entrar en explicaciones más matemáticas haremos una aproximación informal que nos permita leer la ecuación aunque no usemos el cálculo.
La forma más habitual Veremos que no es la única. de la ecuación de Slutsky es \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} = \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} - \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot x_1(p_1, p_2, m) \]
Para facilitar la legibilidad, en ciertos casos no explicitamos los argumentos de las funciones escribiendo $(\cdot)$ Seguiremos poniendo $(\cdot)$ para no olvidar que estamos hablando de funciones. Pero cuidado, esta simplificación de la notación supone que el lector tiene claro cuáles son esos argumentos para cada función. En particular, no debe olvidar que los precios son argumentos para todas las funciones de demanda, pero las demandas ordinarias dependen de la renta $m$, esto es, $x_1(\cdot)=x_1(p_1, p_2, m)$, mientras que las demandas compensadas dependen de la utilidad $u$: $h_1(\cdot) = h_1(p_1, p_2, u)$. en su lugar:
\[ \frac{\partial x_1(\cdot)}{\partial p_1} = \frac{\partial h_1(\cdot)}{\partial p_1} - \frac{\partial x_1(\cdot)}{\partial m} \cdot x_1(\cdot) \] Nuestro primer objetivo es interpretar cada uno de los elementos que aparecen en la ecuación, para después poder interpretar la expresión completa.
Si no estás familiarizado con el uso de las derivadas, en este punto basta con saber (recordar) que el valor de una derivada es el valor del cociente entre lo que cambia el valor de una función y la variación en el argumento que la ha provocado. El matiz que incorpora la derivada es que calcula ese cociente para una variación muy pequeña (infinitesimal) del argumento. Por tanto, el valor de la derivada nos dice cuánto cambiaría (aproximadamente) el valor de la función por cada unidad que aumentara el argumento.
Por ejemplo, en el primer elemento de la ecuación tenemos que, para una pequeña variación del precio, $\Delta p_1$ \[ \frac{\partial x_1(\cdot)}{\partial p_1} \simeq \frac{\Delta x_1^*}{\Delta p_1} \]
(donde $\Delta x_1^*$ es la variación de la demanda ordinaria del bien 1 causada por la variación del precio.)
Haciendo lo mismo con los otros elementos tenemos una nueva versión Llamada versión discreta. de la ecuación:
\[ \frac{\Delta x_1^*}{\Delta p_1} \simeq \frac{\Delta h_1}{\Delta p_1} - \frac{\Delta x_1^{**}}{\Delta m} \cdot x_1^* \]
($\Delta h_1$ es la respuesta de la demanda compensada a un cambio en el precio, $\Delta x_1^{**}$ es la respuesta de la demanda ordinaria a un cambio en la renta, y $x_1^*$ es la cantidad del bien 1 inicialmente demandada).
En el primer elemento de la ecuación tenemos $\Delta x_1^*$. Hemos dicho que es la respuesta de la demanda ordinaria a la variación del precio. Pero eso es lo mismo que decir que es el Efecto Total (sobre el bien 1) de la variación del precio. Al dividir la variación de $x_1$ entre la variación del precio, el valor del cociente $\frac{\Delta x_1^*}{\Delta p_1} $ es el Efecto Total expresado en tanto por uno: cuánto cambia la demanda de bien 1 por unidad monetaria de subida del precio.
Ejemplo
El efecto total ha sido una reducción de cuatro unidades del bien por cada euro de subida del precio.
¿Y si el precio hubiera subido de 10 a 10.5 y la demanda responde bajando de 20 a 18? Sol.
Supón ahora que lo que ha ocurrido es que el precio baja tres euros y la demanda responde aumentando en 6 unidades. ¿Cuál es el efecto (en tanto por uno)? Sol.
Leemos el resultado, -2, como lo que se reduce la cantidad demandada por euro de subida del precio, aunque como en este caso el precio baja, el resultado es que la demanda aumenta en 2 por cada euro que baja el precio.
Siguiendo la misma lógica, sabemos que ante un cambio en el precio de un bien, $\Delta p_1$, las variaciones de las funciones de demanda compensada, $\Delta h_1$ y $\Delta h_2$, nos dan el Efecto Sustitución (para cada bien). El cociente de variaciones, $\frac{\Delta h_1}{\Delta p_1}$, será el Efecto Sustitución expresado en tanto por uno, esto es, variación de la demanda compensada por euro de subida del precio.
El tercer elemento es algo más complejo. Por definición, el Efecto Total es la suma del Efecto Sustitución y el Efecto Renta. Así, el último sumando en nuestra expresión, $-\frac{\Delta x_1^{**}}{\Delta m} x_1^*$, debería ser el Efecto Renta (expresado también en variación de demanda por euro de subida del precio). Vamos a analizarlo.
Si una variación en la renta, $\Delta m$, provoca una respuesta en la demanda, que llamaremos $\Delta x_1^{**}$, el cociente $\frac{\Delta x_1^{**}}{\Delta m}$ sería la respuesta de la demanda ordinaria por cada euro de aumento de la renta.
¿Cuántos euros habría que dar al consumidor para compensarle si el precio del bien 1 sube en un euro? La cesta inicial costaría ahora $x_1^*$ euros más.* Hemos visto anteriormente que la compensación necesaria para mantener su nivel de satisfacción (utilidad) es algo menor que la que permitiría comprar la cesta inicial. Pero cuanto menor es la variación del precio, la diferencia entre ambas formas de calcular la compensación va siendo menor, y la auténtica ecuación de Slutsky se expresa en derivadas, esto es, para una variación muy pequeña (infinitesimal) del precio. Por tanto, para compensar la pérdida de poder adquisitivo de una subida de un euro en $p_1$ habría que dar al consumidor $x_1^*$ euros.
Pero el Efecto Renta es el efecto de deshacer la compensación, esto es, de quitarle los $x_1^*$ euros que le habríamos dado para compensarle. Por tanto, la subida del precio en un euro supone para el consumidor una variación en su poder adquisitivo por valor de $-x_1^*$ euros. Si cada euro que cambie la renta tiene un efecto sobre la demanda según hemos visto arriba, podemos concluir que el Efecto Renta es igual al producto de los euros que cambia el poder adquisitivo por el efecto cada euro sobre la demanda \[ (-x_1^*) \cdot \frac{\Delta x_1^{**}}{\Delta m} \]
Aunque ordenado de otra manera, la expresión anterior se corresponde con el último sumando de la ecuación de Slutsky.
Podemos afirmar pues que la ecuación de Slutsky recoge la descomposición del Efecto Total en la suma de Efecto Sustitución y Efecto Renta, expresados todos ellos como respuesta de la demanda por euro de subida en el precio.
Para la obtención formal de la ecuación de Slutsky necesitamos establecer un resultado previo.
La maximización de la utilidad y la minimización del gasto son dos problemas diferentes, pero están fuertemente relacionados. De manera informativa, sin pretender profundizar en el tema, en Optimización Matemática se afirmaría que cada uno es el problema dual del otro
Observa la figura.
En términos de cálculo, si nos piden que calculemos el mejor punto de la recta $m_0$ usaríamos la ecuación de la recta de balance y la condición de tangencia. Si nos piden que minimicemos el gasto de alcanzar la utilidad $u_0$ usaremos la ecuación de la curva de indiferencia y la condición de tangencia. Y en los dos casos obtendríamos como resultado el mismo punto.
Digámoslo de otra forma. Sea $u_0$ la máxima utilidad que el consumidor puede alcanzar si dispone de una renta $m_0$. Si ahora el problema es alcanzar la utilidad $u_0$ de la forma más barata posible, el resultado será $m_0$. Y eso es así porque en los dos casos la solución resulta ser el mismo punto, el de tangencia entre la curva $u_0$ y la recta $m_0$.
Así, da lo mismo si partimos de una renta $m_0$ cualquiera y $u_0$ es la máxima utilidad alcanzable para esa renta, o si elegimos una utilidad $u_0$ y calculamos la renta $m_0$ necesaria para alcanzar esa utilidad. Podemos afirmar que Desarrollamos la explicación con las demandas del bien 1, pero el mismo razonamiento es aplicable al bien 2: \[h_2(p_1, p_2, u_0) = x_2(p_1, p_2, m_0)\] \[ h_1(p_1, p_2, u_0) = x_1(p_1, p_2, m_0) \]
Para obtener la ecuación de Slutsky partimos de una utilidad cualquiera $u$. El gasto mínimo necesario para alcanzar esa utilidad nos lo da la función de gasto. La expresión anterior quedaría * Observa que antes usábamos el subíndice 0 para emparejar cada nivel de utilidad concreto con su correspondiente nivel de renta. Ahora, al usar la función de gasto, podemos prescindir del subíndice, ya que para cada posible valor de $u$ la función de gasto calcula, automáticamente, el correspondiente valor de la renta. \[ h_1(p_1, p_2, u) = x_1(p_1, p_2, e(p_1, p_2, u)) \]
Derivamos ahora la expresión respecto de $p_1$, para recoger el efecto de un cambio en el precio del bien 1 (en el lado derecho habrá que usar la regla de la cadena). \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} = \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} + \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot \frac{\partial e_1(p_1, p_2, u)}{\partial p_1} \]
El lemma de Shephard nos permite sustituir $\frac{\partial e_1(p_1, p_2, u)}{\partial p_1} = h_1(p_1, p_2, u)$ \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} = \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} + \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot h_1(p_1, p_2, u) \]
Y como inicialmente $m=e_1(p_1, p_2, u) $, se cumple que $ h_1(p_1, p_2, u) = x_1(p_1, p_2, m) $, de donde \[ \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} = \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} + \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot x_1(p_1, p_2, m) \]
Ya sólo tenemos que reordenar para tener la ecuación de Slutsky, tal como la habíamos enunciado. \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} = \frac{\partial h_1(p_1, p_2, u)}{\partial p_1} - \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot x_1(p_1, p_2, m) \]
Ejemplo
Conocemos las funciones de demanda, ordinarias y compensadas, de John (función de utilidad $\mathrm{U}(C, N) = C \cdot N$) \[ C(p_C, p_N, m) = \frac{m}{2 p_C} \quad \quad N(p_C, p_N, m) = \frac{m}{2 p_N} \] \[ h_C(p_C, p_N, u) = \sqrt{\frac{p_N}{p_C}\cdot u} \quad \quad h_N(p_C, p_N, u) = \sqrt{\frac{p_C}{p_N}\cdot u} \]
Queremos comprobar el cumplimiento de la ecuación de Slutsky para una situación inicial con renta $m=300$ conchas y unos precios $p_C=10$ y $p_N=10$.
Ahora habrá que derivar la demanda compensada, para después evaluarla. Sol.
Ya hemos calculado antes que la demanda inicial era $C(10. 10, 300) = 15$.
Ya podemos calcular el Efecto Renta, que será, \[ -\frac{\partial C(p_C, p_N, m) }{\partial m} C(p_C, p_N, m) = - 0.05 \cdot 15 = - 0.75 \]
¿Qué signo tendrán los valores de los distintos elementos que aparecen en la ecuación de Slutsky?
En el capítulo anterior vimos que un bien podía ser Normal o Inferior, Ordinario o Giffen, Substitutivo o Complementario de otro, dependiendo de cómo respondan las demandas a variaciones en la renta o los precios. Vimos también que aunque eran tres clasificaciones distintas, no eran totalmente independientes entre sí. La ecuación de Slutsky no va a cambiar las conclusiones a las que llegábamos entonces, fundamentalmente fijándonos en las figuras, pero sí nos va a permitir explicarlas de manera más sencilla.
Para empezar, podemos hablar con más propiedad del signo de los efectos.* Por ejemplo, en el capítulo anterior llegamos a decir que el efecto sustitución siempre tiene signo negativo. Pero inmediatamente debíamos aclarar que lo que queríamos decir es que ante una variación en el precio de un bien el efecto sustitución sobre ese mismo bien tiene signo contrario a la variación del precio. Si el precio sube el ES lleva a consumir menos, pero si el precio baja lleva a consumir más.
Tomemos el primer elemento que aparece en la ecuación de Slutsky, \[ \frac{\partial x_1(p_1, p_2, m )}{\partial p_1} \]
Ya hemos dicho que su valor es el Efecto Total por euro de subida del precio del bien 1 sobre la demanda de dicho bien. Y que, como en cualquier derivada, ese valor corresponde al del cociente $\frac{\Delta x_1^*}{\Delta p_1} $ para una variación del precio muy pequeña. ¿Qué signo tendrá el valor obtenido, positivo o negativo? Si no tienes clara al respuesta piensa primero en esta otra pregunta: ¿Qué significaría que $\frac{\partial x_1^*}{\partial p_1} > 0$ (esto es, un valor positivo)? Sol.Dado que es un cociente, tendrá signo positivo si numerador y denominador tienen el mismo signo. Por tanto significaría que al subir el precio, $\Delta p_1>0$, la respuesta sería un aumento del consumo, $\Delta x_1 > 0$. Igualmente, si baja el precio bajaría el consumo del bien, de forma que el cociente de dos variaciones negativas daría un cociente positivo. ¿Tienes ahora una respuesta para la pregunta inicial? ¿Crees que el cociente tendrá valor positivo? Sol.
Cuando expresamos el Efecto Total en tanto por uno (como derivada o como cociente de variaciones) el signo nos dice si el bien es Ordinario (signo negativo) o Giffen (signo positivo).
$\textrm{Bien Ordinario: }\frac{\partial x_1(\cdot )}{\partial p_1} < 0 \quad$ $\textrm{Bien Giffen: }\frac{\partial x_1(\cdot )}{\partial p_1} > 0$
El Efecto Sustitución viene dado por la derivada parcial de la demanda compensada, $ \frac{\partial h_1(\cdot )}{\partial p_1}$. Aquí no hay duda en cuanto a su signo. Siempre que suba el precio del bien 1 aumenta la pendiente de las rectas isocoste, y la convexidad de las curvas de indiferencia hace que tengamos que buscar el punto de tangencia subiendo por la curva hacia la izquierda. Eso significa reducir el consumo de bien 1 (y aumentar el de bien 2). Por tanto podemos afirmar que siempre \[ \frac{\partial h_1(\cdot )}{\partial p_1} < 0 \]
Es a este signo al que se refiere la expresión "el Efecto Sustitución siempre es negativo".
¿Y el signo del Efecto Renta?
El signo de la derivada $ \frac{\partial x_1(\cdot )}{\partial m}$ depende de si estamos ante un bie Normal o Inferior. Si el bien es Normal, a mayor renta mayor consumo, tendremos $ \frac{\partial x_1(\cdot )}{\partial m} > 0$. Si es Inferior, el signo de la derivada será negativo. Pero el Efecto Renta no es sólo esa derivada. Así,
Bien Normal:
\[ \frac{\partial x_1(\cdot )}{\partial m} > 0 \Longrightarrow - \frac{\partial x_1(\cdot )}{\partial m} \cdot x_1(\cdot) < 0 \Longrightarrow \mathrm{Efecto \; Renta \; Negativo } \]
Bien Inferior:
\[ \frac{\partial x_1(\cdot )}{\partial m} < 0 \Longrightarrow - \frac{\partial x_1(\cdot )}{\partial m} \cdot x_1(\cdot) > 0 \Longrightarrow \mathrm{Efecto \; Renta \; Positivo} \]
Recuerda que el Efecto Renta en este caso es la respuesta de la demanda causada por la pérdida de poder adquisitivo que ocasiona una subida de un euro en el precio del bien 1. Al tener menos poder de compra el consumidor reduciría su consumo de un bien Normal y aumentaría el de un bien Inferior.
La ecuación de Slutsky nos permite recuperar un par de afirmaciones que ya hicimos anteriormente.
"Si un bien es Normal seguro que es Ordinario (es imposible que sea Giffen)."
En su momento justificábamos esta afirmación gráficamente, viendo que ER y ES apuntarían en el mismo sentido. Pero la ecuación de Slutsky nos permite afirmarlo con más rotundidad: En el razonamiento gráfico podríamos dudar si estamos viendo un ejemplo concreto pero otro ejemplo podría mostrar otra cosa. Si un bien es Normal su Efecto Renta es negativo. Sumado a un Efecto Sustitución que es negativo siempre, la suma sólo puede ser un Efecto Total negativo, esto es, un bien Ordinario.
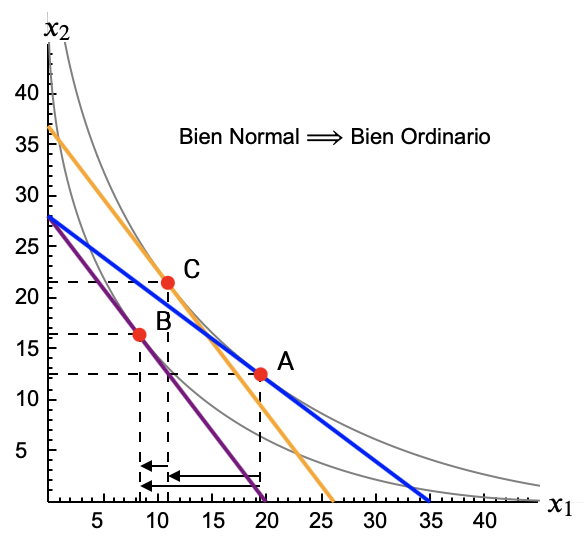
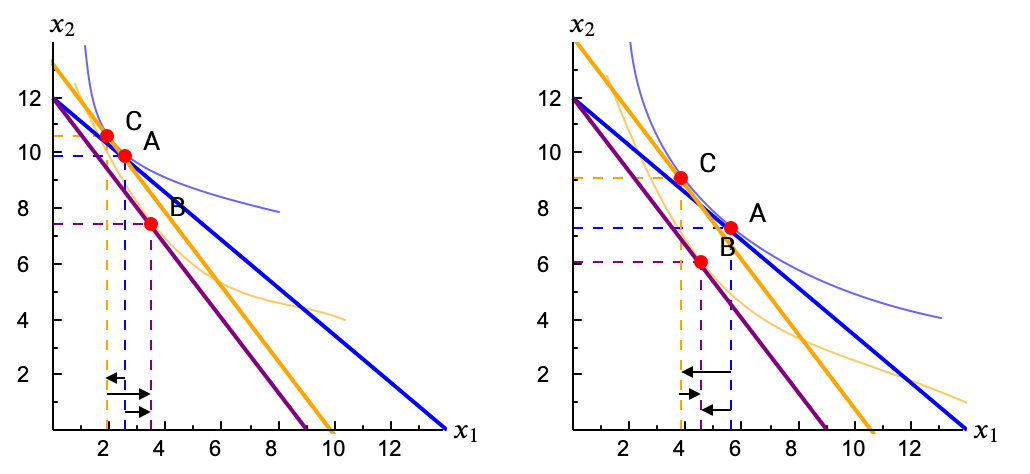
"Si un bien es Inferior puede ser Ordinario o Giffen. Depende del tamaño de los efectos."
De nuevo, el razonamiento gráfico nos decía que cuando el bien es Inferior los efectos Sustitución y Renta apuntan en sentido contrario. En la ecuación de Slutsky lo vemos mediante los signos de los elementos que la forman. Si el bien es Inferior, el signo del Efecto Total no está determinado con carácter general, al ser la suma de un Efecto Sustitución negativo y un Efecto Renta positivo. El signo del Efecto Total será negativo (bien Ordinario) si el Efecto Sustitución es más fuerte (mayor valor absoluto) que el Efecto Renta. En caso contrario el bien será Giffen (Efecto Total positivo).
La ecuación de Slutsky que hemos planteado descompone el efecto de una variación en $p_1$ sobre la demanda del bien 1. Pero la variación de $p_1$ tiene (o puede tener) también efecto sobre la demanda del bien 2. Y, por otra parte, podríamos también preguntarnos por el efecto de un cambio en $p_2$.
En realidad sería más apropiado hablar, en plural, de las ecuaciones de Slutsky.
Para hablar del efecto de un cambio en $p_2$ sobre la demanda de bien 2 no deberían hacer falta más explicaciones, pues diríamos exactamente lo mismo que hemos visto hasta ahora sin más que cambiar los subíndices (en lugar de referirse al bien 1 hay que referirse al bien 2).
\[\frac{\partial x_2(p_1, p_2, m)}{\partial p_2}= \frac{\partial h_2(p_1, p_2, u)}{\partial p_2} - \frac{\partial x_2(p_1, p_2, m)}{\partial m} \cdot x_2(p_1, p_2, m) \](Si no usas el cálculo, puedes ver cualquier derivada anterior como cociente de variaciones, por ejemplo, $\frac{\partial x_2(p_2)}{\partial p_2} \simeq \frac{\Delta x_2}{\Delta p_2}$, teniendo en cuenta que las variaciones del denominador son muy pequeñas)
Para los efectos cruzados, Efecto del cambio en el precio de un bien sobre la demanda del otro bien. sí hay una cuestión que merece explicación.
Supongamos que varía $p_2$ y nos fijamos en el efecto sobre la demanda del bien 1. La ecuación sería: \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_2} = \frac{\partial h_1(p_1, p_2, u)}{\partial p_2} - \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot x_2(p_1, p_2, m) \]
Si nos interesa lo que ocurre con la demanda de bien 1, ¿por qué aparece el último elemento, $x_2(\cdot)$? Para responder a esa pregunta debemos recordar por qué está ahí ese elemento. Recogía la compensación de renta necesaria para mantener el poder de compra cuando el precio subía un euro. Esa compensación era igual al número de unidades consumidas del bien cuyo precio cambiaba. Esto es, al subir $p_2$ en un euro habría que compensar al consumidor con $x_2$ euros.
De manera equivalente, tendremos una cuarta ecuación,
\[ \frac{\partial x_2(p_1, p_2, m)}{\partial p_1} = \frac{\partial h_2(p_1, p_2, u)}{\partial p_1} - \frac{\partial x_2(p_1, p_2, m)}{\partial m} \cdot x_1(p_1, p_2, m) \]La obtención y la interpretación detallada de cada una de las nuevas ecuaciones sigue la misma lógica que vimos para la primera. Hacerlas por escrito puede ser un buen ejercicio para mejorar y asentar la comprensión.* Además algunos profesores la ven como una buena forma de preguntar la teoría en los exámenes.
Volvemos con John, que tiene función de utilidad $\mathrm{U}(C, N) = C \cdot N$, funciones de demanda ordinaria \[ C(p_C, p_N, m) = \frac{m}{2 p_C} \quad \quad N(p_C, p_N, m) = \frac{m}{2 p_N} \]
y de demanda compensada \[ h_C(p_C, p_N, u) = \sqrt{\frac{p_N}{p_C}\cdot u} \quad \quad h_N(p_C, p_N, u) = \sqrt{\frac{p_C}{p_N}\cdot u} \]
¿Puedes comprobar el cumplimiento de la ecuación de Slutsky para el efecto de una variación en $p_C$ sobre la demanda de nubes?* En el ejemplo anterior comprobábamos la ecuación para unos datos concretos. Ahora no nos dan datos. Se trata de comprobarla para cualquier vector de precios y renta.
Ahora ya podemos comprobar si se cumple la ecuación. Sustituyendo los elementos que forman el lado derecho tenemos \[ \frac{\partial h_N(\cdot)}{\partial p_C} -\frac{\partial N(\cdot) }{\partial m} C(\cdot) = \sqrt{\frac{u}{4p_C p_N}} - \frac{1}{2 p_N} \cdot \frac{m}{2 p_C} = \sqrt{\frac{u}{4p_C p_N}} - \frac{m}{4 p_C p_N}\]
Pero en el punto óptimo la utilidad alcanzada se obtiene como resultado de consumir las demandas ordinarias: \[ u = \mathrm{U}(C(\cdot ), N(\cdot )) = \frac{m}{2 p_C} \cdot \frac{m}{2 p_N} = \frac{m^2}{4 p_C p_N} \]
Sustituyendo en la expresión anterior \[ \sqrt{\frac{\frac{m^2}{4 p_C p_N}}{4p_C p_N}} - \frac{m}{4 p_C p_N} = \sqrt{\frac{m^2}{16 p_C^2 p_N^2}} - \frac{m}{4 p_C p_N} = 0 \]
Tras operar en el lado derecho hemos obtenido un valor de 0, lo que confirma el cumplimiento de la ecuación, pues en el lado izquierdo teníamos $\frac{\partial N(\cdot) }{\partial p_C} = 0 $
Normalmente se habla en singular de la ecuación de Slutsky aunque como acabamos de ver en realidad son cuatro. Son cuatro en el caso de dos bienes. En un escenario con $n$ bienes podríamos plantear $n^2$ ecuaciones. Lo más habitual es ver escrita la primera, con el efecto de $p_1$ sobre $x_1$, pero sabemos que las demás están ahí.
Por otra parte, cuando se trabaja de manera más formal se puede expresar la ecuación de Slutsky (ahora sí en singular) como una ecuación matricial.
\[ \begin{bmatrix} \frac{\partial x_1(\cdot )}{\partial p_1} & \frac{\partial x_1(\cdot )}{\partial p_2} \\ \frac{\partial x_2(\cdot )}{\partial p_1}& \frac{\partial x_2(\cdot )}{\partial p_2} \end{bmatrix} = \begin{bmatrix} \frac{\partial h_1(\cdot )}{\partial p_1} & \frac{\partial h_1(\cdot )}{\partial p_2} \\ \frac{\partial h_2(\cdot )}{\partial p_1}& \frac{\partial h_2(\cdot )}{\partial p_2} \end{bmatrix} - \begin{bmatrix} \frac{\partial x_1(\cdot )}{\partial m} \\ \frac{\partial x_2(\cdot )}{\partial m} \end{bmatrix} \cdot \begin{bmatrix} x_1(\cdot )& x_2(\cdot ) \end{bmatrix} \]Aunque va más allá del nivel de este curso, expresar precios y demandas como vectores, o trabajar con matrices de derivadas parciales, permite expresar de manera compacta modelos con más de dos bienes y facilita también el trabajo informático. Aquí se presenta a título ilustrativo, que puede resultar interesante a los más amantes de las matemáticas.
Antes de acabar volvamos una vez más sobre los signos de los elementos que forman las ecuaciones de Slutsky.
Lo que hemos visto para la relación entre $p_1$ y $x_1$ se aplicará directamente a la relación entre $p_2$ y $x_2$. Pero algunas cosas cambian al hablar de los efectos cruzados.
Veamos, por ejemplo, el efecto de un aumento de $p_2$ sobre la demanda del bien 1 (el efecto de $p_1$ sobre el bien 2 se razonaría igual; no lo repetiremos). La ecuación correspondiente es, según hemos visto, \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_2} = \frac{\partial h_1(p_1, p_2, u)}{\partial p_2} - \frac{\partial x_1(p_1, p_2, m)}{\partial m} \cdot x_2(p_1, p_2, m) \]
Siempre será positivo. El Efecto Sustitución siempre dice que al subir el precio de un bien se aumente el consumo del otro bien.
Recuerda la expresión "el Efecto Sustitución siempre es negativo". Debe quedar claro que se refiere al efecto del precio de un bien sobre su consumo. El Efecto Sustitución cruzado, del precio de un bien sobre el consumo de otro, siempre será positivo.
El signo de $\frac{\partial x_1(p_1, p_2, m)}{\partial m}$ depende, como sabemos, de si el bien es Normal (signo positivo) o Inferior (signo negativo).
¿Qué significa ese signo? Sol.
La derivada de una función se interpreta igual que el cociente de variaciones, para una variación pequeña de $x$
\[ \frac{\mathrm{d} y(x)}{\mathrm{d} x} \simeq \frac{\Delta y}{\Delta x} \]La siguiente tabla muestra la relación entre el tipo de un bien ante una variación de la renta (bien Normal o Inferior) y el tipo del mismo bien ante una variación de su precio (bien Ordinario o Giffen), utilizando los signos de la ecuación de Slutsky.
Aquí, "ER grande" se refiere al caso en que el Efecto Renta es, en valor absoluto, mayor que el Efecto Sustitución.
\[|\mathrm{ER}|>|\mathrm{ES}|\]Aquí, "ER pequeño" se refiere al caso en que el Efecto Renta es, en valor absoluto, menor que el Efecto Sustitución.
\[|\mathrm{ER}|<|\mathrm{ES}|\]ES = Efecto Sustitución.
ER = Efecto Renta.
ET = Efecto Total.
Además, los signos de la ecuación de Slutsky permiten estudiar la relación entre el tipo de un bien ante un cambio en la renta (Bien Normal o Inferior) y su efecto cruzado ante un cambio en el precio del otro bien (Complementario o Sustitutivo del otro bien).
Aquí, "ER grande" se refiere a que el Efecto Renta es, en valor absoluto, mayor que el Efecto Sustitución.
\[|\mathrm{ER}|>|\mathrm{ES}|\]Aquí, "ER pequeño" se refiere a que el Efecto Renta es, en valor absoluto menor que el Efecto Sustitución.
\[|\mathrm{ER}|<|\mathrm{ES}|\]Ecuaciones de Slutsky Efectos cruzados Signo del ES Signo del ER Signo del ET