El problema de minimización del gasto
1.- Minimización del gasto
1.- Minimización del gasto

Nos situamos en nuestro escenario habitual, donde un consumidor obtiene su satisfacción del consumo de los bienes 1 y 2, que están disponibles en el mercado a precios $p_1$ y $p_2$. Una función de utilidad, $\mathrm{U}(x_1, x_2)$ representa las preferencias del consumidor.

Pero ahora, el problema que se plantea es conseguir alcanzar cierto nivel de utilidad $u$ de la forma más barata posible. Minimizar el gasto puede parecer un problema menos natural que la maximización de la utilidad, pero situaciones como las que abrían la Introducción tampoco son tan extrañas.

Ejemplo

Papá y mamá quieren organizar la fiesta de cumpleaños de su hijo. Desde luego que quieren una fiesta lo más animada y divertida posible. ¿Qué combinación de globos, comida, chuches...? ¿Cuántos invitados? ¿Alquilar un local o se puede hacer en casa? ¿Y contratar un mago?

Distintas personas tendrán diferente idea de lo que significa suficientemente animada, y pueden tener diferentes preferencias sobre globos, chuches, malabaristas o payasos diabólicos. Las preferencias serán importantes a la hora de tomar la decisión, pero seguramente el coste también formará parte de la decisión.

Una opción es fijar de antemano una cantidad de dinero e intentar sacarle el máximo partido. Pero otra alternativa es calcular el coste de diferentes posibilidades que se consideren satisfactorias y quedarse con la más económica.

El problema en términos gráficos

Como en cualquier problema de decisión, tenemos que identificar las alternativas, establecer un criterio que las compare (de acuerdo con el objetivo) y usar dicho criterio para seleccionar la mejor opción.

El primer paso es sencillo. Puesto que hay que se trata de alcanzar un nivel de utilidad concreto, $u$, las alternativas a considerar son todas las combinaciones de bienes, $(x_1, x_2)$ que alcanzan esa utilidad, esto es, que satisfacen la ecuación \[ \mathrm{U}(x_1, x_2) = u \]

La anterior expresión no es más que la ecuación de la curva de indiferencia de nivel $u$. Por tanto, gráficamente el conjunto de alternativas del problema son los puntos que forman la curva de indiferencia $u$.

Ejemplo

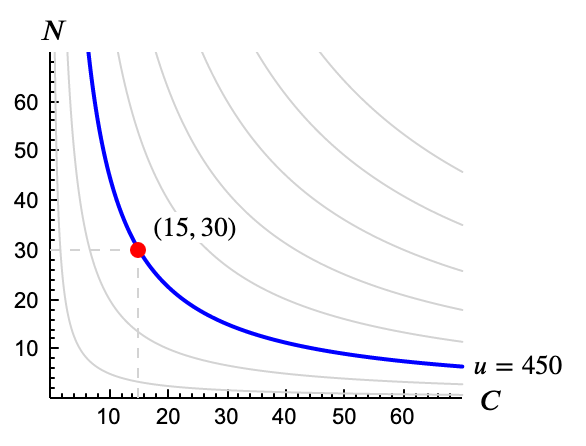
En la Introducción veíamos a John y sus hermanos recién comenzadas sus vacaciones tropicales. El abuelo no quería que John estuviera peor que en casa, donde consumía 15 caramelos y 30 nubes. Con la función de utilidad de John esa cesta le daba una utilidad $\mathrm{U}(15, 30) = $450.

Así, los puntos igual de satisfactorios para John son todos los que tengan utilidad 450, esto es, los que cumplen la ecuación \[ C \cdot N = 450 \]

Despejando $N$ (para la representación gráfica) tenemos que el problema consiste en buscar el punto más barato de la curva 450

El segundo paso, establecer el criterio de comparación entre alternativas, tampoco es complicado, aunque necesita un poco más de elaboración.

Dado que el objetivo es gastar lo menos posible, habrá que calcular lo que costarían las distintas alternativas, y representarlo gráficamente.

Ejemplo 

Para obtener el valor de mercado de una cesta cualquiera, $(x_1^0, x_2^0)$, usamos los precios: \[ p_1 \cdot x_1^0 + p_2\cdot x_2^0 = C_0 \]

$C_0$ es lo que costaría comprar esa cesta en el mercado, pero hay otras cestas que cuestan lo mismo. Serán todas las combinaciones $(x_1, x_2)$ que cumplan la ecuación* Debe quedar clara la diferencia entre esta ecuación y la anterior. Mientras aquella calculaba el coste de una cesta concreta, esta es la que cumplen distintas cestas que tienen el mismo valor $C_0$. (Por supuesto, la $(x_1^0, x_2^0)$ es una de ellas.) \[ p_1 \cdot x_1 + p_2\cdot x_2 = C_0 \]

Podemos representar gráficamente los puntos que cuestan $C^0$. Para ello en la expresión anterior despejamos $x_2$ (por ser la variable que vamos a colocar en el eje vertical. El resultado es: \[ x_2 = \frac{C_0 - p_1 x_1}{p_2} = \frac{C_0}{p_2} - \frac{p_1}{p_2}x_1 \] ¿Reconoces la forma de esta expresión?Sol.

Tanto $C_0$ como los precios son aquí datos, por lo que estamos ante una recta que corta el eje vertical en $\frac{C_0}{p_2}$ y tiene pendiente $-\frac{p_1}{p_2}$.

Todos los puntos de la recta representada cuestan $C_0$ a precios de mercado, y además cualquier punto por encima de la recta cuesta más (y los que están por debajo menos).* Si no ves esto a primera vista, elige un punto cualquiera de los que están por encima. Tiene las dos coordenadas mayores que algunos de los puntos de la recta (los que están más abajo y a la izquierda). Necesariamente cuesta más.

¿Y si en lugar de elegir un punto inicial lo que elegimos es un coste cualquiera, $C_1$? Podemos buscar, como antes, todos los puntos que podrían comprarse con ese dinero

$ p_1\cdot x_1 + p_2\cdot x_2 = C_1 $ $\quad \Longrightarrow \quad x_2 = \frac{C_1}{p_2} - \frac{p_1}{p_2} x_1 $

Volvemos a tener una recta, con la misma pendiente que la anterior, que recoge los puntos que cuestan lo mismo. Cuanto mayor sea el coste, más arriba estará la recta (y viceversa).

Llamaremos recta isocoste a cada una de las líneas formadas por puntos que cuestan lo mismo. Todo punto del plano es una cesta y tiene un valor de mercado, perteneciendo por tanto a una de esas rectas isocoste. El mapa formado por todas Puesto que todos los puntos pertenecen a una isocoste, hay infinitas. Sólo dibujamos algunas, pero las demás están ahí. las rectas isocoste nos permite ver la ordenación de las cestas en función de su valor de mercado. Un punto que pertenece a una isocoste más alta cuesta más.

Obviamente, el coste de las cestas depende de los precios. Si éstos cambian, el mapa de isocostes cambiará. ¿Cómo? En la figura puedes variar los precios.

Ejemplo

El mapa de isocoste está formado por infinitas rectas paralelas. Con los precios vigentes en la isla, $p_C=3$ y $p_N=6$, qué pendiente tendrán las líneas isocoste?Sol.

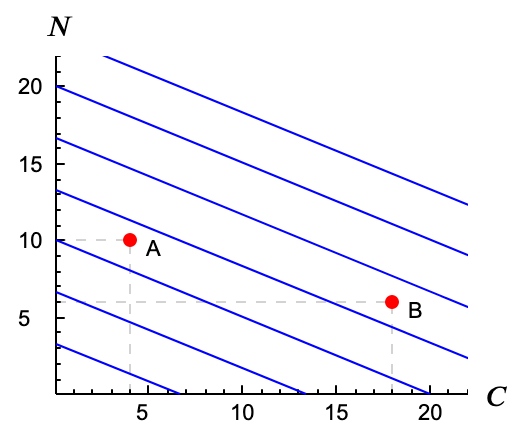
Ya lo habíamos calculado en el ejemplo anterior. Usamos el cociente de precios, $-\frac{p_C}{p_N}-\frac{3}{6} = -0.5$.

Mirando la figura, ¿qué cesta costará más, la $\mathrm{A} = (4, 10)$ or $\mathrm{B} = (18, 6)$? Sol.

Es fácil calcular lo que cuestan, pero aún es más fácil mirar la figura y ver que aunque no estén dibujadas, la isocoste del punto $\mathrm{A}$ está más abajo que la isocoste del punto $\mathrm{B}$. Por tanto la cesta $\mathrm{A}$ cuesta menos.

Podríamos llamar $\mathrm{VM}(x_1, x_2)$ a la función que calcula el valor en el mercado de una cesta de bienes (sin ponerle nombre la hemos usado ya repetidas veces), \[ \mathrm{VM}(x_1, x_2) = p_1 \cdot x_1 + p_2\cdot x_2 \]

$\mathrm{VM}(x_1, x_2)$ es una función que depende de dos variables. Las curvas isocoste son sus curvas de nivel.

Salvo en casos excepcionales de precios que dependen de la cantidad comprada (precios no lineales) las curvas isocoste son en realidad líneas rectas. Es muy habitual hablar directamente de rectas isocoste.

Ahora podemos expresar nuestro problema gráficamente. Buscamos la cesta que consiga cierto nivel de utilidad con el menor gasto posible. Esto es lo mismo que decir, en términos gráficos, que buscamos el punto de la curva de indiferencia que pertenezca a la isocoste más baja posible.

Observa la figura. Puedes usar los deslizadores para elegir un nivel de utilidad y unos precios.

Ahora puedes arrastrar el punto rojo en la figura (sólo podrás moverlo de un punto a otro de la curva). Busca el punto que cueste lo menos posible. Puedes ver a la izquierda el valor de mercado del punto, $\mathrm{VM}(x_1, x_2)$.

¿Has llegado a alguna conclusión sobre cómo buscar el punto óptimo?

El punto más barato es el punto de la curva donde se da la tangencia con una isocoste.

¿Cómo calcular ese punto numéricamente? La clave está en el significado matemático de la palabra tangencia: dos curvas (o una recta y una curva) son tangentes en un punto si en ese punto tienen la misma pendiente. Vuelve a la figura y activa el botón 'Ver RMS'. Coloca el punto rojo en un punto que no sea el de tangencia. La figura muestra la pendiente de las isocoste (el ángulo que mide su inclinación), así como la pendiente de la curva de indiferencia en ese punto (que es la RMS). En cualquier punto de corte son dos ángulos diferentes. Pero si mueves el punto hasta que la isocoste sea tangente verás que los dos ángulos son iguales.* Miden la inclinación de la misma recta, pues la pendiente de una curva en un punto se define como la pendiente de la recta tangente a la curva en ese punto, y en ese punto la isocoste es también la recta tangente.

Lo que acabamos de observar puede resumirse en una ecuación. Si el punto que buscamos es el de tangencia, ha de cumplir que \[ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2}\]

¿Significa esto que ya hemos resuelto el problema? Hablar en términos genéricos puede resultar demasiado abstracto. Mira el ejemplo siguiente.

Example

El abuelo quiere que John alcance la utilidad 450, pero quiere conseguirlo gastando lo menos posible. Ya habíamos calculado la relación marginal de sustitución de John, que resultaba ser* $\mathrm{RMS}(C, N) = -\frac{\mathrm{UMg}_C(C, N)}{\mathrm{UMg}_N(C, N) }$ $\mathrm{RMS}(C,N) = -\frac{N}{C}$. Los precios en la isla son $p_C=3$ and $p_N = 6$.

Podemos escribir la condición de tangencia, que queda \[ -\frac{N}{C} = -\frac{3}{6} \] Pero esta ecuación tiene dos incógnitas y, por tanto, infinitas soluciones. Para cada valor de $C$, hay un valor de $N$ que consigue que se cumpla la ecuación \[ N = \frac{3}{6} \cdot C \]

La condición de tangencia tiene infinitas soluciones. Por sí sola no resuelve nuestro problema. ¿Qué falta para poder calcular las coordenadas del punto óptimo? ¿Sabemos algo más de ese punto que nos pueda ayudar?

Si no tienes clara la respuesta vuelve a la figura y activa el botón 'Más libertad'. Ahora puedes mover el punto libremente por el plano. A la izquierda puedes ver, además del coste del punto, la utilidad que proporciona (recuerda que se trata de alcanzar la utilidad $u$ de la forma más barata posible).

Busca otra vez el punto óptimo. ¿Qué ha cambiado? ¿Es más fácil o más difícil que antes? Cuando vemos la figura reconocemos fácilmente la condición de tangencia como requisito para el punto óptimo. Pero es fácil olvidar algo más básico. Tenemos que elegir un punto que pertenezca a la curva de indiferencia $u$. Y eso se puede traducir (ya lo hemos hecho antes) en una ecuación; la de la curva de indiferencia. \[ \mathrm{U}(x_1, x_2) = u \]

El punto que estamos buscando es el punto de la curva en el que es tangente a una recta isocoste. Podemos calcular ese punto como solución al sistema de ecuaciones: \[ \left. \begin{array}{c} \mathrm{U}(x_1, x_2) = u \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \end{array} \right\} \]

John 

El problema de buscar la forma más barata de alcanzar un cierto nivel de utilidad $u$ puede expresarse fácilmente como un problema de optimización. Concretamente, un problema de minimización sujeto a una restricción no lineal de igualdad, que se resuelve por el método de Lagrange.* Formalmente podría ser más correcto plantear una restricción de desigualdad, $\mathrm{U}(x_1, x_2)\geq u,$. Pero ese problema sería más complejo (Kuhn-Tucker) y en realidad, trabajando con variables continuas, nunca se daría una solución con desigualdad estricta.

\[ \begin{array}{cl} \underset{x_1, x_2}{\mathrm{Min}} &p_1 x_1 +p_2 x_2 \\ \mathrm{s.a.} & \mathrm{U}(x_1, x_2) = u \end{array} \]

Para resolver este problema, construimos la función Lagrangiana, \[ \mathcal{L}(x_1, x_2, \mu) = p_1 x_1 +p_2 x_2 - \mu \cdot ( \mathrm{U}(x_1, x_2)- u) \] E igualamos las derivadas parciales a cero (condiciones de primer orden). \[ \frac{\partial \mathcal{L}(x_1, x_2, \mu) }{\partial x_1} = p_1 - \mu \frac{\partial \mathrm{U}(x_1, x_2) }{\partial x_1} = 0 \] \[ \frac{\partial \mathcal{L}(x_1, x_2, \mu) }{\partial x_2} = p_2 - \mu \frac{\partial \mathrm{U}(x_1, x_2) }{\partial x_2} = 0 \] \[ \frac{\partial \mathcal{L}(x_1, x_2, \mu) }{\partial \mu} = - ( \mathrm{U}(x_1, x_2) - u) = 0 \] Reordenando las ecuaciones y teniendo en cuenta que las derivadas parciales de la función de utilidad son las utilidades marginales, las ecuaciones anteriores se pueden reescribir como: \[ p_1 = \mu \cdot \mathrm{UMg}_1(x_1, x_2) \] \[ p_2 = \mu \cdot \mathrm{UMg}_2(x_1, x_2) \] \[ \mathrm{U}(x_1, x_2) = u \] Finalmente, dividiendo la primera ecuación por la segunda, el sistema se reduce a \[ \left. \begin{array}{c} \frac{p_1}{p_2} = \frac{\mathrm{UMg}_1(x_1, x_2)}{\mathrm{UMg}_2(x_1, x_2)} \\ \\ \mathrm{U}(x_1, x_2) = u \end{array} \right\} \]

La primera ecuación es equivalente a la condición de tangencia, $\mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2}$, por lo que el sistema de ecuaciones que hemos obtenido es exactamente el mismo que habíamos deducido de la gráfica.

Plantear el problema matemático de optimización nos recuerda la existencia en este tipo de problemas de unas condiciones de segundo orden. No entramos aquí en la discusión matemática de estas condiciones, pero sí diremos que con preferencias monótonas y estrictamente convexas la convexidad de las curvas de indiferencia garantiza que la solución del sistema lleve efectivamente a un punto de mínimo coste.

Michael (Math) 

Casos especiales

Como ya pasaba en la maximización de la utilidad, hay algunas preferencias con las que la condición de tangencia no funciona. En casos como los de Mary o Peter era preciso replantear el problema desde el principio para razonar una solución.

Veremos tres ejemplos. Puede haber casos diferentes, pero si comprendes bien esos tres estarás en condiciones de resolver otros.

Mary 

En los bienes complementarios perfectos, como es el caso de Mary, la condición de tangencia no funciona porque la relación marginal de sustitución ni siquiera está definida. Pero eso no significa que el problema no tenga solución. Se resuelve fácilmente observando la representación gráfica de curva de indiferencia y mapa de isocostes.

Con una función de utilidad $\mathrm{Min}\left\{a\cdot x_1, b\cdot x_2\right\}$ (donde $a$ y $b$ son números positivos) la curva de indiferencia $u$ es* Si no lo recuerdas puedes ver una explicación detallada una curva en L con el vértice en $(\frac{u}{a}, \frac{u}{b})$.

Las isocoste son rectas con pendiente dada por el cociente de precios. El punto de la curva de indiferencia que pertenece a una isocoste más baja es el vértice. Todos los demás puntos de la curva de indiferencia contienen unidades de uno de los bienes que no se van a consumir, por lo que no comprarlas ahorra dinero sin perder utilidad.

Aunque no se da la igualdad de pendientes lo que vemos en la figura es algo parecido a la tangencia, en el sentido que a nosotros nos interesa. En el vértice la isocoste toca a la curva sin cortarla. En todos los demás puntos la curva de indiferencia y la isocoste se cortan.

Veamos un segundo caso.

Peter 

En los bienes sustitutivos perfectos la relación marginal de sustitución es la misma en todos los puntos. Las curvas de indiferencia son líneas rectas. En general, la función de utilidad de los sustitutivos perfectos puede expresarse como $\mathrm{U}(x_1, x_2)= a\cdot x_1 + b\cdot x_2$, donde $a$ y $b$ son números positivos. La relación marginal de sustitución es constante, $\mathrm{RMS}(x_1, x_2) = -a/b$.

Si el cociente de precios (pendiente de las isocoste) resultara ser igual al cociente entre $a$ y $b$ (pendiente de la curva de indiferencia), todos los puntos de la curva de indiferencia pertenecerían a la misma isocoste, esto es, costarían lo mismo.

Si los dos cocientes son distintos, lo son en todos los puntos, por lo que la condición de tangencia no se cumple en ninguno. ¿Qué hacemos entonces? La representación gráfica puede ayudarnos una vez más.

¿Cuál es en la figura el punto más barato de la curva de indiferencia? Sol.

El que pertenece a una isocoste más baja. Inicialmente es el corte con el eje vertical, pero si has movido los precios puede haber cambiado.

Estamos ante una solución de esquina. El mínimo coste se alcanza en un extremo del conjunto de alternativas (la curva de indiferencia). Observa que en el óptimo curva de indiferencia y recta isocoste tampoco se cortan en este caso (lo harían si fuera posible moverse más allá del eje, pero no lo es).

El tercer ejemplo puedes verlo de dos maneras. Una posibilidad es ver la figura y las explicaciones de debajo. La otra forma es hacer click sobre la figura para ver el planteamiento y solución más en detalle. Incluye más trabajo matemático.

En la figura puedes ver dos curvas de indiferencia correspondientes a las utilidades 200 y 625. Para la curva más alta la solución se da en un punto donde la isocoste es tangente a la curva de indiferencia.

En la curva más baja buscar la tangencia nos llevaría a la parte negativa de $x_2$, por debajo del eje horizontal. Como eso no es una solució aceptable para nosotros, vemos que el punto más barato está en la solución de esquina, en el corte de la curva de indiferencia con el eje horizontal. En ella no se cumple la tangencia, pues las pendientes son diferentes.

La condición de tangencia es nuestra herramienta favorita. Pero debemos estar preparados para encontrar casos en que no resulte adecuada. Funciona siempre con las preferencias Cobb-Douglas (John).* Y con cualquier otra que, como las Cobb-Douglas, tenga curvas de indiferencia estrictamente convexas que no corten los ejes. Con otras no funciona nunca, como en los casos de complementarios perfectos (Mary) y los sustitutivos perfectos (Peter). Y hay casos como el del último ejemplo, o como las preferencias cuasi-lineales (¿recuerdas a Sandra?) en que la solución puede ser de tangencia o de esquina, dependiendo de los datos concretos de precios y utilidad a alcanzar.

Lo importante es no perder la perspectiva: nuestro problema es buscar el punto más barato de la curva de indiferencia.

Resumiendo

Recta isocoste   Mapa de isocostes
Problema de la minimización del gasto

Cuestiones de Autoevaluación


Anterior  Volver  Siguiente