Hemos estudiado cómo reacciona la demanda del consumidor ante una variación del precio. Esta reacción permite ver que, según las preferencias, un bien puede ser Ordinario o Giffen para un consumidor. También, que un bien puede ser Sustituto o Complementario del otro. Además, nos ha permitido construir una herramienta importante, como es la curva de demanda.

Sin embargo, hay una pregunta que no nos hemos planteado: ¿Por qué el consumidor cambia su decisión cuando varía el precio? En términos matemáticos, la respuesta es obvia. El precio es uno de los datos del problema del consumidor, y si en un problema cambia algún dato, es lógico que eso cambie el resultado.

Pero esa respuesta es demasiado aséptica. El problema matemático que proponemos incluye una cuestión económica, y nos gustaría tener una explicación económica de lo que significa un cambio en el precio. Aparecerán elementos interesantes.

Una vez más, comenzaremos con un ejemplo. Haz clic en la figura (y trabájala sin prisa, porque motiva el resto de la página).

El objetivo del ejemplo es mostrarnos que la variación del precio hace cambiar el problema del consumidor de dos maneras distintas. Por un lado cambia el conjunto de alternativas entre las que puede elegir. Si el precio sube el conjunto se hace menor y la cesta elegida inicialmente deja de ser una opción. Si el precio baja puede comprar cestas que antes no podía. Seguir comprando la cesta inicial dejaría dinero sin gastar, lo que con preferencias monótonas no tendría sentido.

Por otro lado sabemos que la decisión del consumidor pide que, en la cesta elegida, la valoración subjetiva del consumidor del bien 1 en unidades de bien 2, la $\mathrm{RMS}$, coincida con la valoración en el mercado (el cociente de precios). Si en la decisión inicial se cumplía dicha igualdad (condición de tangencia), al cambiar un precio dejará de cumplirse. Por tanto el cambio de precio sería motivo suficiente para que el consumidor ya no desee comprar la cesta inicial incluso aunque pudiera hacerlo.

Matemáticamente la cesta elegida por el consumidor es la que resuelve el sistema de ecuaciones \[ \left. \begin{array}{c} p_1 x_1 + p_2 x_2 = m \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \end{array} \right\} \quad \Longrightarrow \quad (x_1^A, x_2^A) \]

En un sistema de ecuaciones bastaría con cambiar un dato en una de las ecuaciones para que el valor de la solución varíe. En este caso un cambio en $p_1$ modifica las dos ecuaciones.

En el nuevo sistema cambia tanto la ecuación presupuestaria (que determina las posibilidades) como la condición de tangencia. \[ \left. \begin{array}{c} p_1' x_1 + p_2 x_2 = m \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1'}{p_2} \end{array} \right\} \quad \Longrightarrow \quad (x_1^B, x_2^B) \]

Cuando vemos la respuesta del consumidor a una variación del precio estamos viendo una respuesta que es la suma de lo que serían las dos respuestas parciales a los cambios de una y otra ecuación. Nos gustaría descomponer esa respuesta (efecto total) para identificar la parte que corresponde al cambio en el poder adquisitivo y la que se debe a la variación en la tasa de intercambio que ofrece el mercado.

El efecto sustitución

Empezando por el final, ante una subida de $p_1$, ¿cómo saber que parte de la respuesta observada se debe al cambio en la relación de precios? Será más fácil dar una respuesta si reformulamos la pregunta: ¿Cuál sería la respuesta del consumidor a una subida del precio si su poder adquisitivo no se viera afectado por dicha subida?

Llamaremos Efecto Sustitución (ES) a la reacción del consumidor a una variación en el precio de un bien cuando al mismo tiempo varía la renta en la cantidad necesaria para que no pierda ni gane poder adquisitivo.

Para que la definición anterior sea útil necesitamos establecer exactamente qué quiere decir 'mantener constante el poder adquisitivo'.

Consideremos dos posibles respuestas:

1. Un consumidor mantiene constante su poder adquisitivo si ajustamos su renta para que, tras la variación del precio, pueda comprar la misma cesta que compraba antes.
2. Un consumidor mantiene constante su poder adquisitivo si ajustamos su renta para que pueda comprar, tras la variación del precio, una cesta tan buena como la que demandaba antes.

Las dos respuestas pueden parecer bastante similares, y sin embargo hay una diferencia importante. ¿La ves? ¿Cuál de las dos elegirías tú? Es posible que no sepas con cuál quedarte. Trabaja el ejemplo siguiente y después repetiremos la pregunta.

Ejemplo 

¿Te ha permitido el ejemplo llegar a una conclusión sobre la pregunta anterior? ¿Cuál de las dos propuestas te parece mejor si se trata de 'mantener constante' el poder adquisitivo del consumidor?

Nos vamos a quedar con la segunda. Le daremos al consumidor (o le quitaremos, si el precio ha bajado) una compensación de renta, es decir, la cantidad de dinero que haga falta para que termine consumiendo una cesta indiferente a la inicial. Así la variación de precio no le habría perjudicado ni beneficiado. Gráficamente desplazaremos la nueva recta de balance hasta que sea tangente a la curva de indiferencia inicial.

Si el motivo de la compensación era que no se viera perjudicado, no parece lógico que termine beneficiado. Sería un exceso de compensación.*

Hay que decir de todas formas que, aunque esta respuesta es la más 'elegante' desde el punto de vista teórico, es también más complicada de usar en la realidad. Para calcular la compensación de renta necesitaríamos conocer las preferencias (función de utilidad) y hacer los correspondientes cálculos.

En cambio para la primera propuesta basta calcular el coste de la cesta inicial tras variar el precio.

Que la diferencia entre una y otra forma de calcular la compensación sea más o menos grande, depende de las preferencias.

En otras palabras, relacionamos el poder adquisitivo con la satisfacción que el consumidor puede comprar, más que con la cesta de bienes concreta.

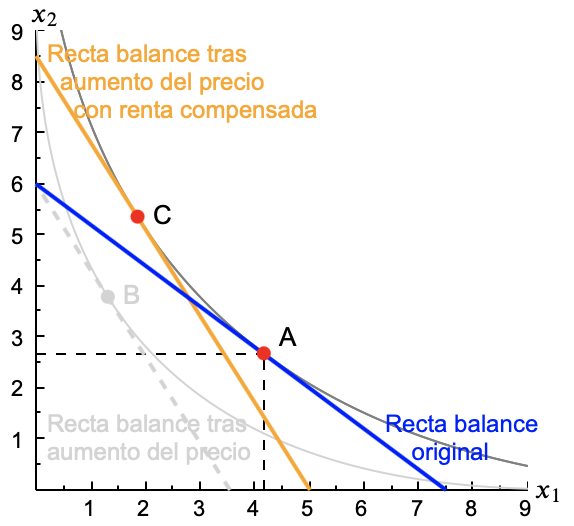
Si nos fijamos en la figura tenemos un punto inicial, A=$(x_1^A, x_2^A)$, óptimo de la recta azul. Que corresponde a unos precios $p_1^0$, $p_2^0$ y una renta $m^0$. La recta de balance naranja corresponde al nuevo precio del bien 1, $p_1' > p_1^0$, acompañada de la compensación en la renta hasta $m^c$ (la recta gris discontinua recoge el nuevo precio pero con la renta inicial $m^0$ sin compensar). Finalmente, el punto C= $(x_1^C, x_2^C)$ es el mejor punto de la recta naranja.

El movimiento desde A hasta C es lo que hemos llamado efecto sustitución. El consumidor se enfrenta a una subida de precio, pero su renta se ha movido para que no pierda poder adquisitivo. El movimiento desde el punto A al punto C lo podemos atribuir en exclusiva al cambio en la relación de precios.

Aunque el caso discutido arriba ha buscado el efecto sustitución de una subida de $p_1$, igualmente nos podríamos haber preguntado por una bajada, o también por una variación de $p_2$. Incluso por una variación simultánea de ambos precios. La lógica sería la misma, compensando la renta para que la variación de precio no afecte a la satisfacción del consumidor. En la siguiente figura puedes ver distintos casos.

• Haz bajar el precio del bien 1 hasta $ p_1'= 1$. Qué pasa con la pendiente de la recta de balance? ¿Cómo es la compensación necesaria en la renta? Sol.
  La pendiente disminuye. El conjunto presupuestario se amplía, por lo que la compensación tendrá que ser negativa. Habrá que quitarle renta para que no gane poder adquisitivo.
  ¿Cómo es el efecto sustitución? Sol.
  El efecto sustitución aumenta el consumo de bien 1 y disminuye el de bien 2.
• ¿Y si, después de volver $p_1'$ a 2, subes el del bien 2 a $p_2'= 4$? ¿Qué pasa en principio con la recta de balance? ¿Y con la compensación? Sol.
  La pendiente disminuye, haciendo el conjunto presupuestario más pequeño. Hará falta darle dinero ($\Delta m > 0$) para que no pierda poder adquisitivo.
  ¿Qué hace el efecto sustitución?Sol.
  Hace aumentar $x_1$ y disminuye $x_2$.
• Compara el efecto sustitución en los dos casos anteriores. ¿Es muy diferente? Sol.
  Aunque al variar los precios las rectas de balance (grises discontinuas) son diferentes, la recta compensada (naranja) es la misma, y por tanto el efecto sustitución también. ¿Sabrías decir por qué? Sol.

  En un caso el poder adquisitivo aumentaba y en el otro se reducía, pero la compensación elimina esa variaciones. Y si te fijas en los cocientes de precios tras la variación, verás que coincide en los dos casos. En el primero $-\frac{1}{2}$ y en el segundo $-\frac{2}{4}$. En ambos casos el efecto sustitución es la respuesta a variar el cociente desde $-\frac{2}{2}= -1$ a $-\frac{1}{2}=-\frac{2}{4}$.
• ¿Y si cambiasen los dos precios a la vez hasta $p_1'=3$ y $p_2'=6$? Sol.
  El cociente de precios final $-\frac{3}{6}$ vuelve a ser $-\frac{1}{2}$. Aunque ha habido un cambio de cesta óptima, la compensación de renta devuelve la decisión al punto inicial. Al no haber cambiado el cociente de precios, no hay efecto sustitución.

Lo que nos enseñan los puntos anteriores (y sus respuestas) es que el efecto sustitución es la respuesta al cambio en la pendiente de la recta de balance, independientemente de qué cambio de precios (en $p_1$, $p_2$ o ambos) lo haya producido. A mayor pendiente menor consumo de bien 1 y mayor consumo de bien 2 (y viceversa).

El Efecto Renta

Para aislar el efecto sustitución hemos compensado la renta del consumidor para mantener constante su poder adquisitivo. Eso nos ha llevado desde el punto inicial, A, hasta el punto C. ¿Qué pasará ahora si deshacemos la compensación, quitándole el dinero que le habíamos dado O devolviéndole el dinero que le habíamos quitado, en el caso de una bajada de precio. ? El consumidor se encontraría al nuevo precio, disponiendo de su renta inicial. Conocemos la solución: el punto B.

Por tanto el paso del punto C al punto B sería la respuesta del consumidor a una variación de renta manteniendo los mismos precios (los nuevos). Y esa variación de renta no es cualquiera, sino la que recoge el impacto de la variación del precio sobre su poder adquisitivo.

Llamamos Efecto Renta (ER) a la respuesta del consumidor al cambio en su poder adquisitivo ocasionado por la variación del precio. Es el resultado de deshacer la compensación de renta que habría mantenido constante el poder adquisitivo.

La figura te permite ver el efecto renta asociado distintos movimientos de precios. Observa que, en realidad, es la misma figura de más arriba, pero centrando el foco en otros elementos.

Independientemente de que aumentes o disminuyas $p_1$ o $p_2$ (o incluso ambos), en la figura siempre se cumple que:

• El punto C es el punto a donde nos ha llevado el efecto sustitución tras compensar la renta del consumidor. Es el mejor punto de la recta naranja, que corresponde al nuevo precio y la renta compensada.
• El punto B es la mejor cesta de la recta púrpura, que corresponde al precio nuevo y la renta inicial (sin compensar).
• La recta naranja y la púrpura son paralelas, puesto que corresponden a los mismos precios. Se diferencian en el nivel de renta.
• Por tanto, el paso de C a B es la respuesta del consumidor a un cambio de renta para unos mismos precios, por eso lo llamamos Efecto Renta.

El Efecto Total

Si miramos las figuras anteriores podemos darnos cuenta de que tenemos un efecto sustitución que nos lleva del punto A al punto C, y un efecto renta que nos lleva del punto C al punto B. El viaje completo ha ido desde el punto A hasta el punto B, como ya habíamos visto al principio.

Lo que hemos hecho ha sido una descomposición del Efecto Total de la variación del precio en dos partes, o efectos parciales. El efecto sustitución recoge la parte de la respuesta que corresponde al cambio en la relación de intercambio entre bienes en el mercado, mientras el efecto renta recoge la respuesta al impacto que la variación del precio tiene sobre el poder adquisitivo de la renta del consumidor.

De esta forma podemos afirmar que la respuesta que 'se ve', que es el efecto total, es la suma de los dos efectos parciales: \[ ET = ES + ER \]

Dado que los efectos son movimientos entre puntos del plano (los vemos como flechas en la figura) formalmente esa suma es en realidad una suma de vectores: \[ \overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB} \]

Cada uno de esos movimientos incluye un componente para las variaciones de bien 1, y otro para las variaciones de bien 2. \[ ET_1 = ES_1 + ER_1 \quad \quad ET_2 = ES_2 + ER_2 \]

Nuestro siguiente paso será aprender a calcular los efectos en casos concretos. Pero antes, la figura te ofrece explorar una vez más los efectos y la relación que hay entre ellos. Vuelve a ser la misma figura de antes, pero ahora tú puedes elegir que efecto resaltar, o si quieres verlos todos a la vez.

Calculando los efectos

La mejor forma de ver cómo calcular los efectos sustitución y renta es comenzar con un ejemplo. Lo haremos con las preferencias de Amanda, a las que pertenecen las figuras anteriores.

Amanda 

Recopilando lo aprendido en el ejemplo, para calcular el efecto total de una variación en $p_1$ y su descomposición en Efecto Sustitución y Efecto Renta, seguimos una serie de pasos.

1. Calculamos el punto demandado inicialmente, A, y el punto demandado tras la variación del precio, B.

   Podemos usar las funciones de demanda, si las tenemos, o resolver el problema del consumidor para los datos iniciales y para los nuevos valores (el nuevo precio).

2. Necesitamos calcular el punto C:
   • Calculamos el valor de la utilidad inicial evaluando la función de utilidad en el punto A: $ \quad u_A$
   • Escribimos la ecuación de la curva de indiferencia inicial, igualando la función de utilidad al valor obtenido para el punto A: $\quad \mathrm{U}(x_1^A, x_2^A) = u_A$
   • Planteamos la condición de tangencia igualando la relación marginal de sustitución al nuevo cociente de precios: $\quad \mathrm{RMS}(x_1, x_2) = -\frac{p_1'}{p_2}$
   • Resolvemos el sistema formado por las dos ecuaciones para obtener el punto C.
3. Una vez que tenemos los tres puntos ya podemos calcular los efectos: \[ ET_1 = x_1^B - x_1^A \quad \quad ET_2 = x_2^B - x_2^A \] \[ ES_1 = x_1^C - x_1^A \quad \quad ES_2 = x_2^C - x_2^A \] \[ ER_1 = x_1^B - x_1^C \quad \quad ER_2 = x_2^B - x_2^C \]

La figuras que hemos usado para explicar los efectos, y también el ejemplo calculado, corresponden a las preferencias de Amanda. Como ya hemos visto anteriormente, diferentes preferencias pueden dar lugar a distintos tipos de respuesta. ¿También los efectos sustitución y renta serán distintos?

Veamos un par de ejemplos.

John 

John no es un tipo problemático, aunque sí nos ha mostrado una curiosidad respecto al caso de Amanda.* En realidad que los efectos sustitución y renta cruzados se anulen entre sí es una característica de las preferencias Cobb-Douglas. Con Mary las cosas suelen resultar menos convencionales.

Mary 

Una vez que hemos visto actuar en varios ejemplos los efectos sustitución y renta nos podemos plantear una nueva pregunta:

¿Los distintos efectos que estamos observando se comportan igual en todos los consumidores?

Ya hemos estudiado el Efecto Total Aunque entonces no lo llamábamos 'total' todavía. de variaciones en os precios, y sabemos que la respuesta a la pregunta anterior es negativa. No todos los consumidores responden de la misma manera a la variación de un precio. Para algunos consumidores un bien puede ser Ordinario, y para otros Giffen. También puede ser Sustitutivo o Complementario del otro bien. ¿Qué podemos decir sobre los efectos sustitución y renta?

¿Hacia dónde va el efecto sustitución?

Cuando las curvas sean estrictamente convexas no hay duda. Si sube el precio de un bien, el efecto sustitución llevará a reducir su consumo y aumentar el consumo del otro bien (si el precio baja será al revés).

Para justificar la afirmación anterior basta ver la figura en la que representamos el efecto sustitución. Cuando el precio cambia compensamos la renta hasta que la nueva recta es tangente a la curva de indiferencia inicial. Esto significa que buscar el punto C es en realidad buscar el punto de la curva inicial que tiene una relación marginal de sustitución (pendiente de la curva) igual al nuevo cociente de precios (pendiente de la recta de balance).

En una curva con pendiente negativa y convexa para buscar un punto con mayor pediente tendré que subir por la curva, hacia la izquierda. Bajando por la curva, hacia la derecha, la $\mathrm{RMS}$ será cada vez menor.* Ya habíamos visto la propiedad de la relación marginal de sustitución decreciente como una forma alternativa de hablar de la convexidad de las curvas de indiferencia.

En la figura, puedes ver lo que pasa con el efecto sustitución cuando 'juegas' con los precios.

El efecto sustitución es la respuesta al cambio en la pendiente de la recta de balance, una vez compensada la renta para eliminar la variación del poder adquisitivo. A mayor pendiente $-\frac{p_1}{p_2}$, independientemente de si es por subir $p_1$ o por bajar $p_2$, el efecto sustitución llevará a consumir menos bien 1 y más bien 2.

Hay una expresión que puedes encontrar en la mayoría de libros de Microeconomía que se graba fácilmente en la memoria, pero tiene cierto 'peligro':

"El efecto sustitución siempre es negativo".

Recordar esta expresión está bien, siempre que se tenga claro su significado, en dos aspectos:

1. El signo negativo quiere decir que el efecto sustitución mueve la demanda de un bien en sentido contrario al movimiento del precio. Se refiere en realidad al signo negativo del cociente entre la variación de la cantidad del bien y la variación de precio que la ha originado: $\frac{SE_1}{\Delta p_1} < 0 $.
   Una subida de precio dará lugar a una variación negativa de la cantidad, mientras una bajada de precio daría lugar a un aumento de la cantidad.

   Ejemplo

   Supongamos que una bajada del precio en 2 libras, $\Delta p_1 = -2$, da lugar a un efecto sustitución que aumenta $x_1$ en 5 unidades, $ES_1= 5$.

   Aunque el efecto sustitución es un aumento, esto es, una variación positiva, el cociente de variaciones sería $\frac{SE_1}{\Delta p_1} = \frac{5}{-2}$.

   Cuando decimos que el efecto sustitución es siempre negativo no nos referimos al signo de $SE_1$, sino al signo del cociente. Precio y cantidad se mueven en sentido contrario.

2. No debemos olvidar que el efecto sustitución tiene dos componentes. El efecto sobre el bien 1 y el efecto sobre el bien 2. Si sube $p_1$ el efecto sustitución reduciría $x_1$, y al mismo tiempo aumentará $x_2$. Cuando decimos que el efecto sustitución es negativo debemos tener claro que nos estamos refiriendo al efecto sustitución sobre el bien cuyo precio cambia. El efecto sustitución cruzado, del precio de un bien sobre la demanda del otro bien, será positivo: $\frac{SE_2}{\Delta p_1} > 0$.

Finalmente, ¿qué pasará cuando las soluciones no sean de tangencia? Hay casos, como el de Mary, en el que el efecto sustitución simplemente no existe. Y puede haber otros, cuando aparecen soluciones de esquina, en que hay que ir con especial cuidado para calcular los efectos. Pero incluso en los casos 'raros' nunca vamos a encontrar que al subir al precio el efecto sustitución aconseje aumentar el consumo del bien.

¿Y qué podemos decir sobre el signo del efecto renta?

El efecto renta es la respuesta del consumidor cuando deshacemos la compensación de renta que habría mantenido constante su poder adquisitivo. En definitiva, el efecto renta es la respuesta a un cambio de renta. Y sabemos que distintos consumidores pueden responder a un cambio en su renta de forma diferente.

Una subida de $p_1$ o de $p_2$ reduce el poder adquisitivo del consumidor. Si para el consumidor el bien 1 es Normal el efecto renta le llevará a consumir menos de ese bien. Si es Inferior le llevará a consumir más. (Lo mismo pasará con el bien 2).

Dicho de forma más general, el efecto renta de una subida de precio llevará a reducir la cantidad consumida de los bienes Normales, y a aumentar la de los Inferiores.

Con la misma advertencia de antes, podemos decir que para un bien Normal cualquier variación de precio* da igual si es su propio precio o el de otro bien. da lugar a un efecto renta negativo (esto es, $\frac{ER_1}{\Delta p_1} < 0$ and $\frac{ER_1}{\Delta p_2} < 0$). Si el bien es Inferior el efecto renta sería positivo ($\frac{ER_1}{\Delta p_1} > 0$ and $\frac{ER_1}{\Delta p_2} > 0$).

En la figura el bien 1 es Inferior mientras que el bien 2 es Normal. Observa el efecto renta sobre cada bien (cada eje) cuando varíes un precio.

(En todas las figuras que habíamos visto hasta ahora los dos bienes eran Normales.)

Juntando los efectos

Cuando estudiábamos el efecto de una variación en la renta, establecimos la clasificación de los bienes en Normales e Inferiores. Viendo el efecto (total) de un cambio en el precio dijimos que los bienes puede ser Ordinarios o Giffen, Sustitutivos o Complementarios.

Ahora que sabemos que detrás (o dentro) del efecto total de la variación de un precio hay un efecto renta, podemos establecer alguna relación entre las clasificaciones que antes habíamos hecho de forma independiente.

¿Cómo un bien puede ser Giffen?

Para las siguientes cuestiones nos dicen que el bien 1 Usamos el bien 1 pero todo lo que vamos a decir sería válido cambiando los subíndices, para el bien 2. es Normal para un consumidor:

• ¿Cómo será el efecto renta sobre el bien 1 de una subida de $p_1$? Sol.
  Puesto que una subida de precio le hace perder poder adquisitivo, el consumidor reducirá la demanda de cualquier bien Normal. Por tanto \[ ER_1 < 0 \] (También hay un efecto sobre el bien 2, del que no nos ocupamos ahora.)
• ¿Y cómo será el efecto sustitución?Sol.
  Una subida de $p_1$ encarece el bien 1 respecto al bien 2 (aumenta la pendiente de la recta de balance) lo que llevará al efecto sustitución hacia la izquierda: \[ SE_1 < 0 \]
• ¿Qué podemos decir del efecto total? Sol.
  El efecto total es la suma del efecto sustitución y el efecto renta. Si los dos efectos parciales son negativos la suma también lo será. \[ ET_1 = ES_1 + ER_1 < 0 \]
  ¿Qué te dice eso sobre el bien 1? Sol.
  Si al subir $p_1$ el efecto renta tiene valor negativo podemos afirmar que para el consumidor el bien 1 es Ordinario.

De las cuestiones anteriores podemos extraer una primera conclusión:

"Si un bien es Normal forzosamente será Ordinario."

Gráficamente, al subir $p_1$ los dos efectos van hacia la izquierda, por lo que su suma también.

Supongamos ahora que el bien 1 es Inferior, y vemos de nuevo el efecto de una subida de $p_1$.

• ¿Cómo será el efecto renta sobre el bien 1? Sol.
  La caída del poder adquisitivo llevará al consumidor a aumentar su consumo del bien Inferior (demandará más al sentirse más pobre): \[ ER_1 > 0 \]
• ¿Y el efecto sustitución?Sol.
  El efecto sustitución siempre dice que al subir el precio se demande menos de ese bien. \[ ES_1 < 0 \]
• ¿Hacia dónde irá el efecto total? Sol.
  Tenemos que $ER_1>0$ y $ES_1 < 0$. Si no tenemos valores concretos no podemos responder a la pregunta, ya que el signo de la suma depende de cuál de los dos efectos sea más fuerte (mayor valor absoluto).
  ¿Qué tipo de bien será el 1? Sol.
  Tenemos que ver el signo del efecto total. Si el efecto renta es más fuerte que el efecto sustitución estaríamos ante un bien Giffen, ya que la suma sería positiva. Si es más fuerte el efecto sustitución la suma es negativa y el bien es Ordinario.

Conclusiones:

"Si un bien es Inferior el efecto renta de una subida de precio irá en sentido contrario al efecto sustitución. Si el efecto renta es más pequeño en valor absoluto el bien será Ordinario. Si el efecto renta es más fuerte que el efecto sustitución el bien será Giffen."

"Para ser Giffen un bien necesita ser Inferior, aunque no cualquier bien Inferior es Giffen."

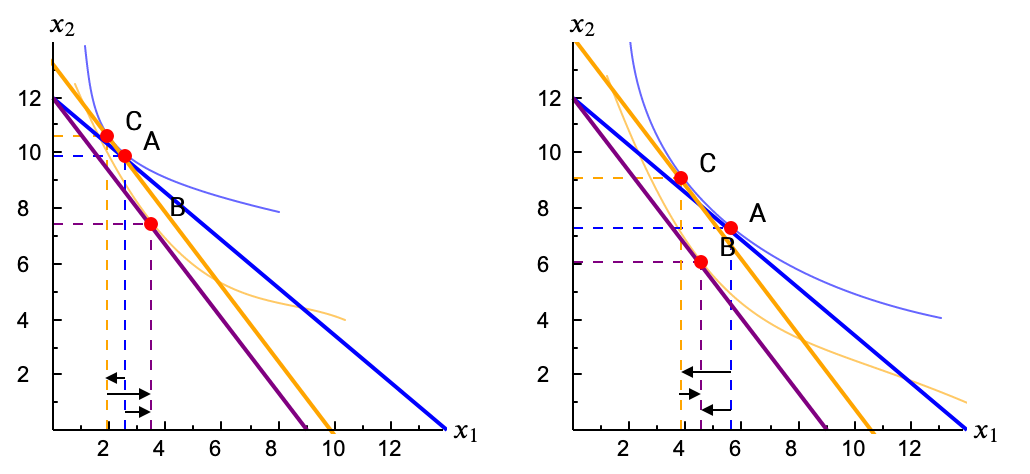
En las figuras puedes ver dos casos diferentes. En las dos el bien 1 es Inferior. Pero sólo en la de la derecha es un bien Giffen.

¿Cómo un bien puede ser Complementario de otro?

Según hemos visto, la convexidad de las curvas de indiferencia hace que el efecto sustitución siempre lleve a reducir el consumo del bien cuyo precio sube, y a aumentar el consumo del otro.

Pero hay casos en que al subir el precio de un bien el consumidor termina consumiendo menos del otro bien. Decimos entonces que el bien 2 es Complementario del 1.

Puede parecer que hay una contradicción entre los dos párrafos anteriores. Pero ten en cuenta que el primero habla del efecto sustitución, $ES_2$, mientras que el segundo habla del efecto total, $ET_2$.

Sabemos que al subir $p_1$ el efecto sustitución sobre el bien 2 tendrá un valor positivo, $ES_2>0$ (ya que al aumentar la pendiente el efecto sustitución sube por la curva hacia la izquierda). ¿Y el efecto renta?

Supongamos que el bien 2 es un bien Inferior:

• ¿Cómo será el efecto renta? Sol.
  Dado que la subida del precio significa una pérdida de poder adquisitivo, el consumidor aumentará su consumo del bien Inferior \[ ER_2 > 0 \]
• ¿Y el efecto total? Sol.
  Puesto que $ES_2 > 0$ y $ER_2 > 0$, forzosamente el efecto total será positivo puesto que es la suma de los dos anteriores. $ET_2>0$
  ¿De qué tipo de bienes estamos hablando? Sol.
  Puesto que al aumentar $p_1$ el efecto total es un aumento de $x_2$, podemos decir que el bien 2 es sustitutivo del 1.

Conclusión:

"Si un bien es Inferior seguro que es Sustitutivo del otro."

¿Y si el bien 2 es un bien Normal?

• ¿Cómo será el efecto renta de una subida de $p_1$? Sol.
  $ER_2$ es el efecto de una pérdida de poder adquisitivo. Si el bien 2 es Normal, el efecto renta será una reducción de la cantidad consumida. \[ ER_2 < 0 \]
• ¿Y hacia dónde irá el efecto total?Sol.

  Tenemos que el efecto sustitución es positivo, $ES_2>0$, y el efecto renta negativo, $ER_2>0$.

  El efecto total es la suma de los dos, y su signo dependerá de los tamaños (valores absolutos) de efecto sustitución y efecto renta.

  ¿Qué podemos decir sobre el tipo de bienes? Sol.

  Si $| ES_2| > | ER_2|$, tendremos que $ET_2 > 0$ y, por tanto, el bien 2 es Sustitutivo del bien 1.

  Si, por el contrario, $|ES_2| < | ER_2|$, el efecto total será negativo, $TE_2<0$, y diremos que el bien 2 es Complementario del 1.

Conclusiones:

"Un bien Normal será Sustitutivo o Complementario de otro bien dependiendo de si el efecto sustitución es más o menos fuerte que el efecto renta."

"Si un bien es Inferior también será Sustitutivo del otro."

Las figuras que hemos ido utilizando para explicar los efectos corresponden a las preferencias de Amanda. Si vuelves a la última (la que te permitía ver los efectos por separado o en conjunto) puedes comprobar que para Amanda el bien 2 es Normal, y aunque el efecto renta de $p_1$ sobre el bien 2 va en sentido contrario al efecto sustitución, éste es mayor por lo que el bien 2 es Sustitutivo del 1.

El caso de Michael era diferente. Comenzamos a verlo en el principio de esta página (volver a ver), justo cuando nos planteamos la existencia de una variación en el poder adquisitivo ocasionada por la variación del precio. Nos hicimos entonces algunas preguntas, pero no llegamos a profundizar en la respuestas. Ahora que tenemos nuevas herramientas, podemos responder con más detalle.

Michael 

A estas alturas los efectos sustitución y renta ya no deberían tener secretos para nosotros. Para ponernos a prueba propondremos un último ejemplo. De hecho corresponde a unas preferencias con las que ya hemos trabajado: las de Sandra.

Sandra 

Resumiendo:

Un cambio en el precio de un bien motiva un cambio en la cesta demandada por el consumidor de dos maneras diferentes: la relación de intercambio entre bienes que ofrece el mercado varía, y además cambia el poder adquisitivo de la renta del consumidor.

Nos interesaría distinguir qué parte de la respuesta observada (Efecto Total) se debe a cada uno de los dos motivos.

• Si variamos la renta del consumidor de forma que su poder adquisitivo se mantenga constante, la respuesta del consumidor será atribuible al cambio en el cociente de precios. Llamamos a esa respuesta Efecto Sustitución.
• Consideramos que el consumidor mantiene constante el poder adquisitivo si tras la compensación de su renta puede comprar una cesta indiferente a la inicial (y ninguna mejor).
• Llamamos Efecto Renta a la respuesta del consumidor cuando se deshace la compensación de la renta. (Deshacer la compensación significa quitarle el dinero recibido para compensar una subida de precio, o devolverle el dinero que se le habría quitado para compensar una bajada de precio.)
• El sentido del efecto sustitución depende únicamente de si el cociente de precios aumenta o disminuye. Un aumento en la relación $\frac{p_1}{p_2}$, llevará al efecto sustitución a reducir el consumo de bien 1 y aumentar el de bien 2.
• El sentido del efecto renta depende de si el bien es Normal o Inferior. Cualquier aumento de precio tendrá un efecto renta negativo para los bienes Normales, y positivo para los Inferiores.
• En un bien Normal el efecto sustitución y el efecto renta sobre el bien cuyo precio cambia van en el mismo sentido (se suman). Un bien Normal no puede ser Giffen. Si el bien es Inferior van en sentido contrario, y el bien puede ser Giffen si el efecto renta es más fuerte que el efecto sustitución.
• Si un bien es Normal los efectos sobre su demanda de un cambio en el precio del otro bien van en sentido contrario. Si el efecto sustitución es más fuerte el bien es Sustitutivo del otro. Si es más fuerte el efecto renta estamos ante un bien Complementario. Un bien Inferior será siempre Sustitutivo (ya que los efectos sustitución y renta sobre su demanda de un cambio en el precio del otro bien van en el mismo sentido).

Poder adquisitivo constante   Compensación de renta
Efecto Sustitución   Efecto renta   Efecto total