|
La demanda del consumidor 4.- Variaciones de precios |
Decimos que nuestros consumidores son 'precio-aceptantes'. Toman sus decisiones dados unos precios fijos En este escenario 'fijos' significa que no dependen de la decisión del consumidor. En particular, el precio por unidad no depende del número de unidades compradas. Tampoco son negociables. vigentes en los mercados. Pero eso no significa que el precio de un bien no pueda cambiar exógenamente. En un problema un cambio exógeno es algo que cambia por causas externas al problema; un cambio en un dato. Ciertamente una posible subida del precio de un bien puede ser el resultado (endógeno) del funcionamiento del mercado. Aunque el consumidor individual es parte de ese mercado, es demasiado pequeño como para que sus decisiones influyan en el resultado final. Por eso el precio es un dato para él, y una variación sería algo exógeno, algo sobre lo que él no tiene control.
Está claro que las opciones al alcance del consumidor dependen de los precios (como estudiamos en el capítulo anterior). Puede que tras un cambio de precios tenga acceso a nuevas cesta que antes estaban fuera de su alcance, o al contrario, que su conjunto de alternativas se reduzca. En cualquier caso, lo más probable es que la cesta demandada por el consumidor tras el cambio sea otra.
La siguiente figura permite variar los precios y ver, o no, la decisión óptima del consumidor. Puedes explorarla un poco, pero lo que haremos a continuación es plantearnos una serie de preguntas para estudiar las diferentes posibilidades de forma ordenada.
Antes de preocuparnos de las decisiones propiamente dichas, estaría bien usar la figura para recordar algunas cosas que ya sabemos pero conviene tener frescas ahora.
Pasemos, ahora sí, a preguntarnos por la respuesta en la decisión óptima del consumidor.
Nos planteamos una pregunta concreta: Si dada una situación inicial se produce una subida de $p_1$, ¿cómo cambiará (si es que lo hace) la cantidad de bien 1 que compra el consumidor?
Ejemplo
Supongamos que John, función de utilidad $\mathrm{U}(C, N) = C\cdot N$, tiene 1.20 libras (expresadas en peniques, $m=120$) para gastar en caramelos y nubes a precios $p_C=3$ y $p_N=4$ peniques. ¿Qué comprará? ¿Cómo respondería su decisión a una subida en el precios de los caramelos hasta $p_C'=5$ ?
Sabemos, por haberla calculado previamente, que la relación marginal de sustitución de John viene dada por la función $\mathrm{RMS}(C, N) = -\frac{N}{C}$, por lo que podemos plantear el sistema formado por la condición de tangencia y la ecuación presupuestaria. Como es un ejercicio que ya hemos hecho varias veces (si no es así deberías hacerlo ahora \[ \left. \begin{array}{c} 3 \cdot C+ 4 \cdot N=120 \\ -\frac{N}{C} = -\frac{3}{4} \end{array} \right\} \] Operando obtenemos \[ C^*=20 \quad \quad N^* = 15 \] ), también podemos recuperar las funciones de demanda de John que habíamos obtenido (funciones de demanda de John).
\[ C(p_C, p_N, m) = \frac{m}{2\cdot p_C} \quad \quad N(p_C, p_N, m) = \frac{m}{2\cdot p_N} \]De una u otra forma, encontramos que con los precios iniciales John compraría la cesta \[ (C^*, N^*) = (20, 15) \]
Con el nuevo precio (y planteando de nuevo el sistema o usando las funciones de demanda) la demanda de John pasa a ser \[ (C', N') = (12, 15) \]
Vemos que ante la subida del precio de los caramelos John reduce su consumo de estos.
En el ejemplo vemos que John reduce su consumo de caramelos cuando sube su precio. ¿Te sorprende esta respuesta? Seguro que no. Nos parece completamente normal que ante una subida del precio un consumidor decida comprar menos (o que ante una bajada del precio compre más). Pero, ¿es esto necesariamente así? ¿Comprarías más sal si su precio bajase? ¿Reducirías tu consumo de antibióticos estando enfermo si su precio sube?
Es cierto que las anteriores preguntas plantean casos especiales, pero ponen de manifiesto que reducir el consumo no es la única respuesta posible a una subida de precio, aunque sí sea la más habitual. Como la palabra "Normal" ya la hemos utilizado (para referirnos a los bienes que el consumidor compra más cuando aumenta su renta) utilizaremos aquí otra que en el lenguaje habitual es un sinónimo. Decimos que un bien es Ordinario para un consumidor si este reduce su consumo del bien cuando su precio sube (y lo aumenta si el precio baja).* Hay palabras que tomamos del vocabulario habitual pero en el contexto de la Microeconomía les damos un significado específico, con el que debemos ser cuidadosos. Aunque podamos considerar que reducir el consumo es 'lo normal' al subir el precio, hemos reservado esa palabra para referirnos a la respuesta ante cambios en la renta. Aunque en el lenguaje habitual 'normal' y 'ordinario' puedan ser sinónimos, en Microeconomía las dos palabras tienen distinto significado
En un ejemplo anterior vimos que los caramelos eran para John un bien Normal. Según acabamos de definir, ahora vemos que también son un bien Ordinario, pues al subir el precio ha consumido menos.
En la figura tenemos las preferencias de Amanda y podemos ver cómo responde a una variación de $p_1$ a partir de una situación inicial.
¿Qué pasa si das a $\Delta p_1$ un valor positivo (esto es, si el precio sube)? El nuevo punto óptimo está más a la izquierda, por lo que podemos concluir que para Amanda el bien 1 es un bien Ordinario.
Antes hemos puesto un par de ejemplos de bienes (sal y antibióticos) que para la mayoría de los consumidores no cumplirían la definición de bien Ordinario Como se dijo al hablar de los bienes Normales o Inferiores, no estamos hablando de los bienes en sí, sino de las preferencias del consumidor sobre los bienes. Un bien que es Ordinario para un consumidor puede no serlo para otro. . El caso de la sal es un bien para el que, dado su bajo precio, la mayoría de los consumidores alcanza su nivel de saciedad. Un nivel de saciedad es aquél a partir del cual el consumidor no mejora consumiendo más. Puede incluso que empeore. Más allá de ese punto las preferencias ya no son monótonas. La decisión de cuánta sal comprar no suele ser en general un problema económico.
En cuanto a los antibióticos ocurre algo parecido. Normalmente la decisión de cuántos consumir no es una cuestión de preferencias, sino de indicación médica. Que sean más o menos baratos no influiría en su demanda por parte del consumidor. Aunque tanto en este caso como en el anterior si el precio subiera lo suficiente podría ocurrir que el consumidor sí se viera obligado a reducir su consumo.
Pero no hace falta buscar motivos especiales. Es posible mostrar preferencias que sin incumplir ninguna de las propiedades habituales (monótonas, continuas, convexas...) llevarían al consumidor a aumentar su consumo ante una subida del precio.
Decimos que un bien es Giffen* En cuanto al término 'Giffen', hace referencia al estadístico escocés sir Robert Giffen (1837-1910) a quien el también economista Alfred Marshall (1842-1924) atribuye la primera descripción del concepto. Si bien es cierto que dicha descripción no aparece en escritos publicados por aquel, ambos autores fueron coetáneos, por lo que no hay por qué dudar de la afirmación de Marshall. para un consumidor si este responde a una subida del precio aumentando su consumo (o reduce el consumo cuando el precio baja).

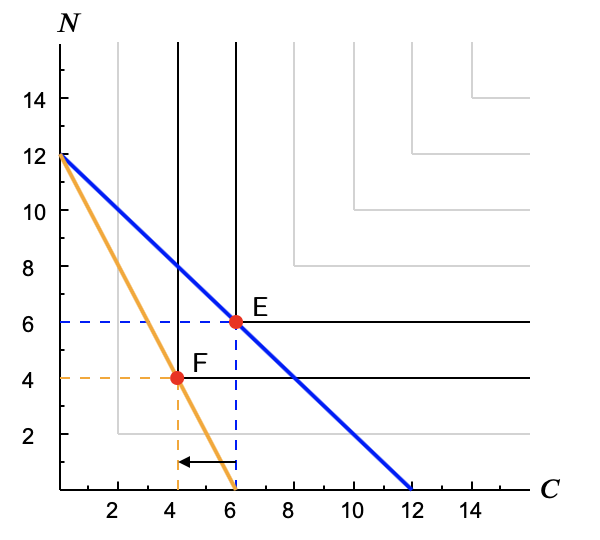
Las curvas de la figura no incumplen ninguna propiedad de las habituales (aunque como ves son un poco raras comparadas con las otras que hemos visto), y muestran un caso de bien Giffen. Al subir $p_1$ el consumidor pasa de E a F, aumentando su consumo de bien 1. Bien es cierto que no tenemos una función de utilidad que mostrar como ejemplo, pero eso no significa que no exista.* Cuando definimos la función de utilidad decíamos que debía asignar un número a cada punto con el requisito de que a punto más preferido mayor número. Vimos que con preferencias monótonas (y continuas) era fácil ver que eso era posible (no se dijo que fuera fácil).
Resumiendo, la respuesta de la cantidad demandada de un bien por un consumidor a una variación en su precio nos permite hablar de bienes Ordinarios o Giffen (para ese consumidor). Si demanda menos al subir el precio estamos ante un bien Ordinario. Si al subir el precio compra más decimos que es un bien Giffen.
Como en la respuesta a la renta, podemos concretar las definiciones anteriores usando las derivadas parciales de las funciones de demanda.
El bien 1 será Ordinario para un consumidor si dada su función de demanda $x_1(p_1, p_2, m)$ se cumple que \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} < 0 \]
Si el signo fuera positivo tendríamos un bien Giffen.
Ejemplo
Las funciones de demanda de Amanda eran \[ x_1(p_1, p_2, m) = \frac{p_2 \cdot m}{p_1\cdot (p_1 + p_2)} \quad \quad x_2(p_1, p_2, m) = \frac{p_1 \cdot m}{p_2\cdot (p_1 + p_2)} \]
Calculando la derivada parcial de $x_1$ respecto de $p_1$ tenemos \[ \frac{\partial x_1(p_1, p_2, m)}{\partial p_1} = p_2 m \frac{-1}{p_1^2 (p_1 + p_2)^2} (2p_1+p_2) < 0 \]
Por lo que podemos afirmar que para Amanda el bien 1 es Ordinario. (Fíjate que en realidad no habría sido necesario hacer la derivada en este caso, pues basta con mirar la función para ver que aumentar el valor de $p_1$ hace más grande el denominador sin que varíe el numerador, por lo que el valor del cociente, que es la cantidad demandada, disminuirá.)
¿Y el bien 2, será Ordinario o Giffen? Sol.
Antes de cerrar el punto, una última cuestión. Si un bien es Giffen, al subir el precio se compraría más. Pero si el precio sigue subiendo, y el consumo sigue aumentando, ¿no llegará un momento en que será imposible aumentar el consumo, ya que la renta es fija? Sol.
Efectivamente, esto es así. Como pasó al hablar de los bienes Inferiores o Normales, tenemos que considerar la propiedad de bien Ordinario o Giffen como algo local, para ciertos valores de precios y renta. Concretamente, no es posible que un bien sea Giffen para todos los precios. Siempre habría un punto a partir del cual el consumidor no tendría más remedio que reducir su consumo al aumentar el precio, incluso si se gasta toda su renta en ese bien.
¿Qué tipo de bien serán los caramelos para Mary?
Sol.
Para responder a la pregunta podríamos también aquí usar las funciones de demanda que habíamos calculado, o bien simplemente fijarnos en la figura.
Dado que el punto elegido por Mary siempre es un vértice, cuando el precio de los caramelos aumente y la recta de balance gire hacia abajo (pivotando sobre el corte con el eje vertical en $\frac{m}{p_N}$), el punto elegido tendrá, sin duda, menos caramelos. Por tanto, estos son un bien Ordinario para Mary.
Vemos también en la figura, que se reduce el consumo de nubes. ¿Significa esto que también las nubes son un bien Ordinario? Sol.
La solución a la cuestión anterior termina fijándose en algo que no debería sorprendernos, pero de lo que no hemos hablado (todavía). En la figura, la variación en el precio de un bien (caramelos) afecta a la demanda del otro (nubes).
En las figuras anteriores (y también en el texto) nos hemos ocupado del efecto de un cambio en $p_1$ sobre la cantidad demandada del bien 1. Pero cuando variábamos $p_1$, en el eje vertical también se daban cambios. Al fin y al cabo cuando escribimos la función de demanda de un bien como $x_2(p_1, p_2, m)$ estamos diciendo que la cantidad que el consumidor comprará de bien 2 no sólo depende de su propio precio, sino también del precio del bien 1. ¿Qué podemos decir sobre esa dependencia cruzada?
Observa la siguiente figura. En ella podemos ver de nuevo el efecto de un cambio en $p_1$ sobre la decisión de dos consumidores diferentes. Pero ahora nos vamos a fijar en lo que ocurre con la cantidad demandada del bien 2, esto es, tendremos que mirar lo que pasa en el eje vertical.
En la parte izquierda tenemos a Amanda, a la que ya conocemos. A la derecha tenemos a Michael, del que enseguida sabremos más.
¿Qué ves al subir el precio del bien 1 (usando el deslizador)?
La figura nos ha mostrado que la respuesta de la demanda de bien 2 a un cambio en $p_1$ depende de las preferencias del consumidor.
Decimos que para un consumidor el bien 2 es Sustitutivo del bien 1 si aumenta su consumo de bien 2 cuando sube el precio del bien 1 (o reduce su consumo de bien 2 cuando baja el precio del bien 1).
Decimos que el bien 2 es Complementario del bien 1 para un consumidor si ante la subida en el precio del bien 1 el consumidor responde reduciendo su consumo de bien 2 (o al bajar $p_1$ aumenta $x_2$).
Podemos definir bienes Sustitutivos y Complementarios usando las derivadas parciales de las demandas:
El bien 2 es Sustitutivo del bien 1 si dada la demanda del bien 2, $x_2(p_1, p_2, m)$, su derivada parcial respecto de $p_1$ es positiva
\[ \frac{\partial x_2(p_1, p_2, m)}{\partial p_1} > 0 \]Decimos que el bien 2 es Complementario del bien 1 para el consumidor si dada la demanda del bien 2, $x_2(p_1, p_2, m)$, su derivada parcial respecto de $p_1$ es negativa\[ \frac{\partial x_2(p_1, p_2, m)}{\partial p_1} < 0 \]
En la mayoría de los casos suele pasar que si el bien 2 es sustitutivo del bien 1, el bien 1 también es sustitutivo del bien 2. Lo mismo ocurre con los complementarios. Por eso a veces se relaja el lenguaje y se suele decir que dos bienes son sustitutivos (o que dos bienes son complementarios), dando por hecho que en las dos direcciones ocurre lo mismo. Sin embargo, aunque pueda parecer raro, puede ocurrir que para un consumidor el bien 1 sea sustitutivo del 2 pero el 2 sea complementario del 1.
Ejemplo
A continuación puedes ver varios ejemplos: Mary, John, Amanda y Michael. Los dos últimos necesitan un poco de cálculo.
Ejemplos:
Mary John Amanda (Mates) Michael (Mates)
¿Son sustitutivos o complementarios? Sol.
En su momento dijimos que las preferencias de Mary eran un ejemplo de bienes Complementarios Perfectos. Los bienes Complementarios Perfectos respondían a una definición concreta; el consumidor sólo obtiene satisfacción de lo consumido en una proporción determinada de los dos bienes, desechando lo que se salga de esa proporción. Eso daba lugar a unas curvas de indiferencia e forma de L, con el vértice en los puntos que contienen la proporción exacta.
Ahora encontramos que las preferencias de Mary también cumplen la definición de bienes Complementarios.
Debe quedar claro que son dos definiciones diferentes. Mary cumple las dos, pero Michael, que hemos introducido como ejemplo de bienes Complementarios, no cumple para nada la definición de Complementarios Perfectos (sus curvas de indiferencia son 'curvas', no en L).
Hemos visto varias figuras, para diferentes preferencias, en las que veíamos la respuesta a un cambio en el precio, en las que hay un punto inicial y un punto final. Pero, como hicimos anteriormente con las variaciones de la renta, nada nos impide completar las figuras incluyendo más de dos posibles valores de $p_1$, con sus correspondientes puntos óptimos. Puedes ver unos cuantos activándolos en la figura.
Dados unos valores fijos de $p_2$ y $m$, cada posible valor de $p_1$ va dando una nueva recta de balance y en esta un nuevo punto óptimo. Si fuéramos añadiendo muchos valores los puntos óptimos irían formando una línea.
Así, dados unos valores fijos de $m$ y $p_2$, llamamos curva precio-consumo del bien 1 a la línea formada por todos los puntos $(x_1, x_2)$ que serían óptimos para algún valor de $p_1$.
Si no lo has hecho todavía, activa en la figura el botón "Curva precio-consumo".
En resumen, la curva precio-consumo del bien 1 nos ha mostrado que para Amanda el bien 1 es Ordinario y el bien 2 es sustitutivo del bien 1. Pero recuerda que no es la única posibilidad.
Veamos ahora la curva precio-consumo del bien 1 de Michael.
Ejemplo
Un caso más sencillo que los anteriores es el de John. Recuerda que sus funciones de demanda eran \[ C(p_C, p_N, m) = \frac{m}{2\cdot p_C} \quad \quad N(p_C, p_N, m) = \frac{m}{2\cdot p_N} \]
Habíamos visto también que para John la demanda de cada bien depende de la renta y del precio, pero no del precio del otro bien. ¿Cómo será su curva precio-consumo para los caramelos? Sol.
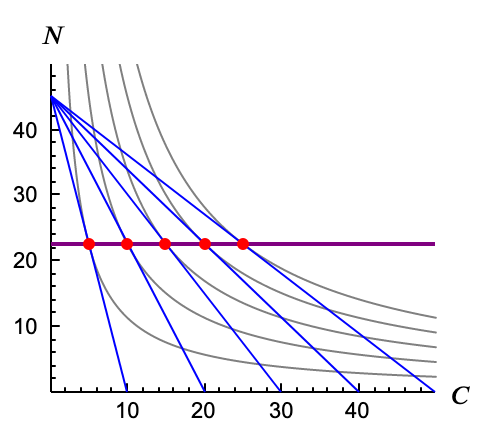
Si damos un valor fijo a $m$ y $p_N$ y vamos cambiando el precio de los caramelos, $p_C$, John demandaría diferente cantidad de caramelos para cada precio, pero mantendría constante su consumo de nubes. La curva precio-consumo será una línea horizontal.
Posiblemente te has dado cuenta de que aunque el título de esta sección habla de 'variaciones en los precios' solamente hemos estado variando $p_1$. ¿Y si lo que varía es $p_2$?
En realidad todo lo que hemos visto para los efectos de un cambio en $p_1$ podría aplicarse a un cambio en $p_2$. La lógica es la misma, aunque ahora veríamos cómo influye $p_2$ en la demanda del bien 2 (¿Ordinario o Giffen?) y en la demanda de bien 1 (¿Sustitutivo o Complementario del bien 2?).
Ejemplo
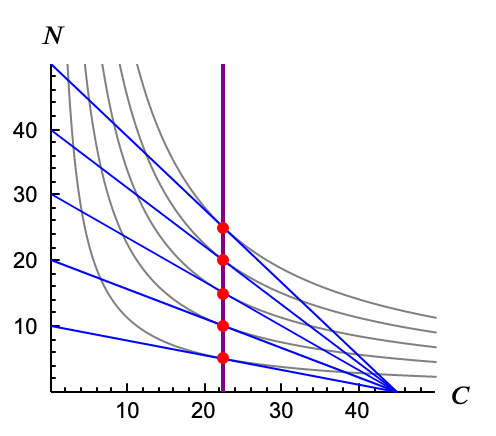
Al variar $p_N$ se iría moviendo la cantidad de nubes, pero no la de caramelos. La figura mostrará una línea vertical
Sí es cierto que, aunque el razonamiento es el mismo, el aspecto de las figuras cambiará. Haciendo 'click' sobre la siguiente figura podrás repasar lo que ya hemos visto, pero con la 'gimnasia mental' de interpretar los distintos movimientos cambiando los ejes.
Un procedimiento habitual cuando queremos profundizar en el resultado de un problema es el que hemos seguido. Una vez alcanzado el primer objetivo, resolver el problema, nos preguntamos cómo cambia su solución cuando cambian los datos. Es lo que hemos estado haciendo con las decisiones de demanda del consumidor.* Aunque en contextos más amplios se llama a esto 'análisis de sensibilidad', en Economía es más habitual hablar de estática comparativa.
Cambiar más de un dato a la vez puede hacer difícil, si no imposible, dar una interpretación interesante del resultado observado. Por eso hemos ido cambiando los datos, $m$, $p_1$ y $p_2$, de uno en uno, en cada caso manteniendo constantes los otros dos. Pero algunos cambios simultáneos pueden resultar interesantes. Un ejemplo: ¿Cómo cambiaría la cesta demandada por un consumidor si duplicamos todos los precios al mismo tiempo que le duplicamos también su renta?
Posiblemente tengas una respuesta intuitiva, que seguramente será correcta, pero como a veces la intuición falla, queremos construir una respuesta argumentada. De hecho vamos a formular dos razonamientos ligeramente diferentes.
El primero, más mecánico, pasa por plantear el sistema de ecuaciones que resuelve el problema del consumidor. La demanda de éste viene dada por la solución al sistema formado por la condición de tangencia y la restricción presupuestaria. Dados unos precios y una renta iniciales, $(p_1^0, p_2^0, m^0)$, tenemos
\[ \left. \begin{array}{c} \mathrm{RMS}(x_1, x_2) = -\frac{p_1^0}{p_2^0} \\ p_1^0 x_1 + p_2^0 x_2 = m^0 \end{array} \right\} \quad \Longrightarrow \quad (x_1^0, x_2^0) \]Al doblar precios y renta tendremos unos nuevos valores, $p_1'=2p_1^0$, $p_2'=2p_2^0$ y $m' = 2m^0$. Tendremos así un nuevo sistema a resolver, \[ \left. \begin{array}{c} \mathrm{RMS}(x_1, x_2) = -\frac{p_1'}{p_2'} \\ p_1' x_1 + p_2' x_2 = m' \end{array} \right\} \quad \Longrightarrow \quad (x_1', x_2') \]
Pero si en la primera ecuación de este nuevo sistema sustituimos los precios y renta en función de los antiguos, tenemos \[ \mathrm{RMS}(x_1, x_2) = -\frac{2p_1^0}{2p_2^0} \quad \Longleftrightarrow \quad \mathrm{RMS}(x_1, x_2) = -\frac{p_1^0}{p_2^0} \] Y en la segunda \[ 2p_1^0 x_1 + 2p_2^0 x_2 =2 m^0 \quad \Longleftrightarrow \quad p_1^0 x_1 + p_2^0 x_2 = m^0 \]
Dado que cada ecuación del nuevo sistema es equivalente a la ecuación del problema inicial, ambos sistemas deben tener la misma solución.\[ (x_1^0, x_2^0) = (x_1', x_2') \]
La conclusión es que al duplicar precios y renta la cesta demandada no cambia.*
En realidad la misma respuesta habría podido obtenerse de forma más sencilla. Sin necesidad de construir el sistema de ecuaciones basta con darse cuenta de que la ecuación presupuestaria es equivalente al duplicar precios y renta: \[ 2p_1^0 x_1 + 2p_2^0 x_2 =2 m^0 \quad \Longleftrightarrow \quad p_1^0 x_1 + p_2^0 x_2 = m^0 \]
Pensando sobre la figura, la ecuación presupuestaria nos da la recta de balance. Esto significa que el conjunto de alternativas al alcance del consumidor (conjunto presupuestario) no se ha modificado. Por tanto el punto que era óptimo inicialmente seguirá siéndolo tras el cambio, ya que las alternativas al alcance del consumidor no han variado.
Este segundo camino no sólo es más simple, sino que además resulta ser más general. Mientras, como ya hemos visto, la condición de tangencia no es aplicable a todas las preferencias, el conjunto presupuestario como conjunto de alternativas no viene de las preferencias, sino solo de la existencia de una renta y unos precios.
Fíjate en que si en todo el razonamiento anterior sustituyes el 2 al definir los nuevos precios y renta por cualquier constante $\alpha$ positiva, $p_1' = \alpha p_1^0$, $p_2' = \alpha p_2^0$, $m'= \alpha m^0$, la conclusión es exactamente la misma.
Según lo que acabamos de ver podemos afirmar que para cualquier consumidor una variación simultánea y en la misma proporción de los precios y la renta no afectará a la cesta demandada. Esta propiedad de las funciones de demanda se conoce como homogeneidad de grado 0 en precios y renta.
El lenguaje de las matemáticas diría que las funciones de demanda de cualquier consumidor serán homogéneas de grado 0 en precios y renta.
Siendo $x_i(p_1, p_2, m)$ la función de demanda del bien $i$ ,donde $i\in \{1, 2\}$, \[ \forall (p_1, p_2, m), \forall \alpha > 0, \quad \quad x_i(\alpha p_1,\alpha p_2, \alpha m) = x_i(p_1, p_2, m) \]
Quizá quieras recordar la definición genérica de homogeneidad de grado $k$ de una función.
En consecuencia, una función cuyo valor varía si cambian en igual proporción los precios y la renta no puede ser una función de demanda.
A continuación puedes comprobar, como ejercicio, que las funciones de demanda de los consumidores con los que venimos trabajando cumplen la homogeneidad de grado 0.
Con John y Mary se ve muy fácil. Con Amanda, Michael o Sandra hay que operar con un poco de cuidado.
John Mary Amanda Michael Sandra
Las funciones de demanda de John son
$C(p_C, p_N, m) = \frac{m}{2\cdot p_C} \quad $ $ \quad N(p_C, p_N, m) = \frac{m}{2\cdot p_N} $
Si multiplicamos por $\alpha$ tanto los precios como la renta tendríamos, para los caramelos, \[ C(\alpha p_C,\alpha p_N,\alpha m) = \frac{\alpha m}{2\cdot \alpha p_C} \]
que se simplifica a \[ \frac{m}{2\cdot p_C} = C( p_C, p_N, m) \]
Lo mismo para las nubes.
Las funciones de Mary eran \[ C(p_C, p_N, m) = \frac{m}{ p_C + p_N} \quad \quad N(p_C, p_N, m) = \frac{m}{ p_C + p_N} \]
También aquí, cuando multiplicamos precios y renta es fácil simplificar para ver que la cantidad demandada tras variar precios y renta es idéntica a la inicial. \[ C(\alpha p_C,\alpha p_N,\alpha m) = \frac{\alpha m}{ \alpha p_C +\alpha p_N} = \] \[ = \frac{\alpha m}{ \alpha (p_C + p_N)} = \frac{m}{ p_C + p_N} = C(p_C, p_N, m) \]
Puedes repetir el proceso para las nubes.
Las funciones de demanda de Amanda son algo más complejas, por lo que habrá que operar un poquito más. \[ x_1(p_1, p_2, m) = \frac{p_2 \cdot m}{p_1\cdot (p_1 + p_2)} \quad \quad x_2(p_1, p_2, m) = \frac{p_1 \cdot m}{p_2\cdot (p_1 + p_2)} \]
De nuevo multiplicamos precios y renta por $\alpha$. Usaremos paréntesis que no serían necesarios para remarcar que aplicamos la función a nuevos precios y renta que son los iniciales multiplicados por $\alpha$, como por ejemplo $p_1'=(\alpha p_1)$.
Comprobamos la propiedad para la demanda de bien 1. Queda para ti repetir el ejercicio con la otra demanda.
\[ x_1(\alpha p_1, \alpha p_2, \alpha m) = \frac{(\alpha p_2) \cdot (\alpha m)}{(\alpha p_1)\cdot ((\alpha p_1) + (\alpha p_2))} = \frac{\alpha^2 \cdot p_2 \cdot m}{\alpha^2 \cdot p_1\cdot ( p_1 + p_2)} = \] \[ = \frac{ p_2 \cdot m}{ p_1\cdot ( p_1 + p_2)} = x_1(p_1, p_2, m) \]Tenemos las demandas de Michael:
\[ x_1(p_1, p_2, m) = \frac{m}{ p_1^{1/2} (p_1^{1/2} + p_2^{1/2})} \quad \quad x_2(p_1, p_2, m) = \frac{m}{ p_2^{1/2} (p_1^{1/2} + p_2^{1/2})} \]Al variar precios y renta usando $\alpha$ tenemos para el bien 1 (de nuevo el bien 2 queda para ti). \[ x_1(\alpha p_1, \alpha p_2, \alpha m) = \frac{(\alpha m)}{ (\alpha p_1)^{1/2} ((\alpha p_1)^{1/2} + (\alpha p_2) ^{1/2})} = \frac{\alpha m}{ \alpha^{1/2} p_1^{1/2} (\alpha^{1/2} p_1^{1/2} + \alpha^{1/2} p_2 ^{1/2})} \] \[ = \frac{\alpha m}{ \alpha p_1^{1/2} (p_1^{1/2} + p_2 ^{1/2})} = \frac{m}{ p_1^{1/2} (p_1^{1/2} + p_2^{1/2})} = x_1(p_1, p_2, m)\]
De nuevo, el bien 2 queda para ti.
¿Qué podemos decir de la respuesta del consumidor a un cambio en los precios?
Bien Ordinario Bien Giffen Bien sustitutivo Bien Complementario Curva precio consumo Homogeneidad de grado $0$