|
La demanda del consumidor 5.- La curva de demanda |
Las curvas de Engel muestran gráficamente la relación entre el nivel de renta y la cantidad demandada de un bien, dados unos precios fijos. Al analizar el efecto de una variación en un precio podemos hacer algo similar. Y esa representación gráfica de la relación entre el precio y la cantidad del bien que el consumidor decide comprar va a ser particularmente importante.* Se podría plantear también la representación de la relación cruzada, del precio de un bien con la cantidad del otro bien. Pero no es algo que tenga demasiado interés, al menos con carácter general. Merece la pena dedicarle una página completa.
Comenzaremos poco a poco, con un ejemplo, antes de pensar más en general.
EjemploSegún hemos visto, el consumidor demanda una cesta de bienes, $(x_1, x_2)$, dependiendo de su renta y de los precios vigentes. Esa cesta viene dada por las funciones de demanda $x_1(p_1, p_2, m)$ y $x_2(p_1, p_2, m)$. Ahora queremos centrarnos en la relación entre $p_1$ y $x_1$. Para ello suponemos unos valores fijos de la rente, $m^0$, y del precio del otro bien, $p_2^0$.* Lo que nos interesa es la relación entre la demanda de un bien y su propio precio. Lo que digamos para la relación entre $p_1$ y $x_1$ será igualmente aplicable a la relación entre $p_2$ y $x_2$ (en este caso permanecerían fijos $m$ y $p_1$).
La relación a representar no será más que el resultado de utilizar los valores fijos, $p_2^0$ y $m^0$, en la función de demanda del bien 1. Al usarlos quedará una función en la que $x_1$ sólo depende de $p_1$. Con una función de sólo una variable podremos representarla gráficamente como una curva, y es por eso la llamaremos curva de demanda.
\[ x_1(p_1, p_2^0, m^0) = x_1(p_1) \] Supongamos que la función de demanda del bien 1 de un consumidor es \[ x_1(p_1, p_2, m) = \frac{m}{p_1 + \sqrt{p_1 p_2}} \]
y tenemos que $m=18$ y $p_2= 2$.
Usando los valores en la función obtenemos la expresión de la curva de demanda, que vemos además representada.
\[ x_1(p_1, 2, 18) = \frac{18}{p_1 + \sqrt{2 p_1}} \]
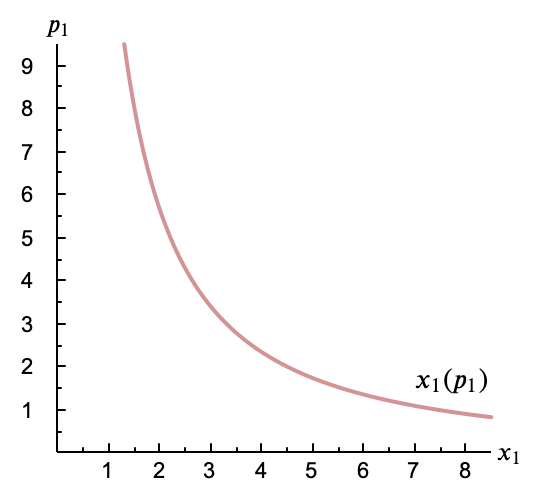
(De hecho esta es la curva que habíamos construido anteriormente en el ejemplo.)
Seguramente, antes de llegar aquí habías hecho algún curso introductorio de economía, y el término 'curva de demanda' no te resulta extraño. Pero en los siguientes párrafos y ejemplos puedes encontrar algunos aspectos en los que probablemente no has pensado. La curva de demanda contiene más información de lo que parece a primera vista.
Acabas de ver representada una curva de demanda. Nos la han dado hecha y seguramente no le ves nada de especial. Como decíamos, casi seguro que no es la primera que ves. ¿Y si hubieras tenido que dibujarla tú? ¿Cómo lo habrías hecho?
EjemploLo primero que debería llamarnos la atención al intentar representar una curva de demanda es que los ejes están alrevés (¿Te habías dado cuenta?) Cuando representamos funciones lo normal es que en el eje vertical veamos el 'resultado' de la función (el valor de la variable dependiente). En las curvas de demanda (también en las de oferta) la cantidad de bien, que depende del precio, está en el eje horizontal.
En realidad colocar los ejes de una u otra forma es una cuestión arbitraria, y si representamos así demandas y ofertas es simplemente por tradición. Pero conviene ser conscientes de ello porque trabajar 'al revés' de lo habitual puede llevarnos a algún error a la hora de interpretar las figuras.* Por ejemplo, en una función $y=f(x)$ con mucha pendiente, un pequeño cambio en la $x$ da lugar a un cambio grande en la $y$. Pero si cambiamos los ejes de posición la curva que antes era muy inclinada ahora tiene muy poca pendiente (la pendiente siempre se refiere a la inclinación respecto a la horizontal).
Operativamente, a la hora de representar gráficamente una curva de demanda lo más habitual es despejar el precio en la expresión de la curva de demanda para después poder aplicar el procedimiento habitual de representación de funciones.
Ejemplo
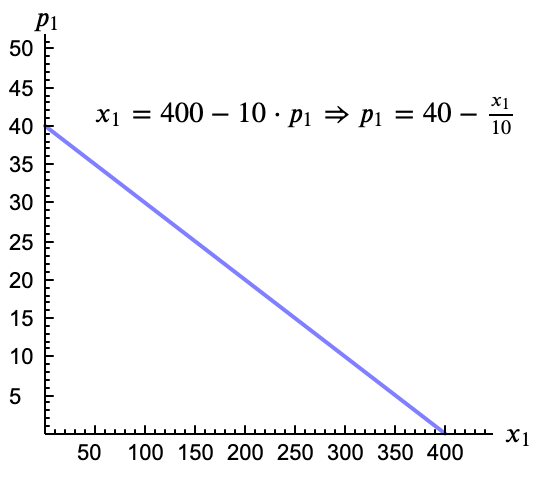
Representa gráficamente la curva de demanda dada por $x_1 = 400- 10 p_1$ Sol.
$p_1 = 40 - 0.1 x_1$
Aunque la curva de demanda de $x_1$ es una relación entre la demanda de un bien y su propio precio, está definida dados unos valores fijos de $m$ y $p_2$. ¿Qué pasaría si $m$ o $p_2$ variaran?
EjemploUn cambio en la renta o en el precio del otro bien darán lugar a una nueva curva de demanda de bien 1. Normalmente decimos que al cambiar uno de esos valores la curva se desplaza. ¿Pero podemos concretar algo más sobre ese desplazamiento?
Supongamos un valor concreto de $p_1$ (el valor de $p_2$ está dado). Si manteniendo esos precios, aumenta la renta, ¿cómo será la respuesta del consumidor? ¿Consumirá más o menos bien 1? Sol.
|
$x_1$ Bien Normal $x_1$ Bien Inferior |
|
$x_1$ Sustitutivo de $x_2$ $x_1$ Complementario de $x_2$ |
Facilitar la representación gráfica no es el único motivo para expresar la curva de demanda escribiendo el precio como función de la cantidad de bien.
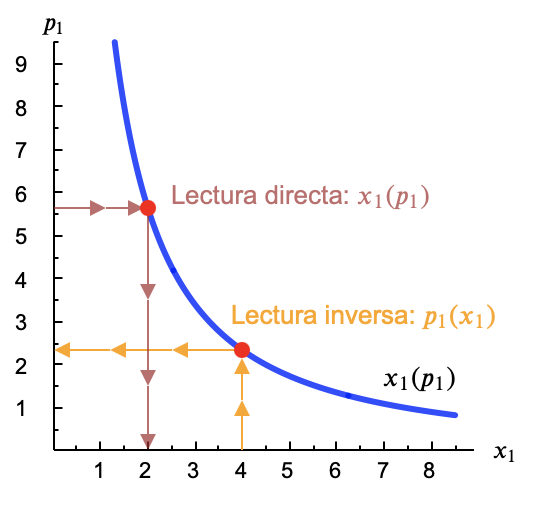
Llamamos curva inversa de demanda a la función que obtenemos al despejar el precio en la curva de de demanda. Así, sería una función que nos dice cuál es el precio al que el consumidor demandaría cada cantidad del bien (dados unos valores fijos de la renta y el precio del otro bien).
Debe quedar claro que no estamos hablando de una nueva curva, sino de otra forma de expresar (leer) la misma curva.
Ejemplo
La función de demanda de Nubes de John es \[ N(p_C, p_N, m) = \frac{m}{2 p_N} \]
Si la renta es $m=100$ (las demandas para cada bien no dependen del precio del otro bien), ¿cuál es la curva inversa de demanda? Sol.
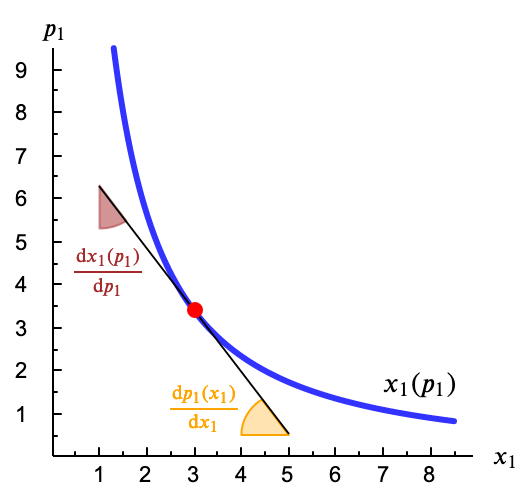
En cuanto a la pendiente de la curva recuerda que corresponde siempre, para pequeñas variaciones, al cociente entre variación vertical y variación horizontal. En este caso $\frac{\Delta p_1}{\Delta x_1}$.
Fíjate que a mayor pendiente (mayor valor del primer cociente) menor respuesta de la cantidad demandada a una subida del precio (valor del segundo cociente).
Cuando colocamos los ejes en la forma habitual en matemáticas, la derivada de la función nos da la pendiente La pendiente en un punto es la tangente trigonométrica del ángulo que forma con la horizontal la recta tangente a la curva en ese punto. de la curva en cada punto.
Pero si colocamos los ejes al revés, con la variable dependiente en el eje horizontal, la derivada nos dará la inclinación respecto a la vertical.
Las matemáticas nos dicen también que dada una función, $y = f(x)$, normalmente Salvo casos especiales con problemas de continuidad. la derivada de la inversa de la función es igual al inverso de la derivada de la función original: \[\frac{\mathrm{d} f^{-1}(y)}{\mathrm{d} y} = \frac{1}{\frac{\mathrm{d} f(x)}{\mathrm{d} x}} \]
Así, tenemos que si $x_1 = x_1(p_1)$ es la curva de demanda y $p_1(x_1)$ es la curva inversa, se cumplirá que \[\frac{\mathrm{d} p_1(x_1)}{\mathrm{d} x_1} = \frac{1}{\frac{\mathrm{d} x_1(p_1)}{\mathrm{d} p_1}} \]
La derivada de la curva inversa de demanda (que es la pendiente en la figura) es igual al inverso de la derivada de la curva (directa) de demanda.
Igualmente podemos decir que la derivada de la curva de demanda nos da el inverso de la pendiente de la curva.
Ejemplo
Hemos visto antes que para John, con $m=100$, la curva (directa) de demanda de nubes era $N=\frac{50}{p_N}$, y la curva inversa: $p_N=\frac{50}{N}$.
Derivando tenemos \[ \frac{\mathrm{d} N(p_N)}{\mathrm{d}p_N} =-\frac{50}{p_N^2} \quad \quad \frac{\mathrm{d} p_N(N)}{\mathrm{d} N} = -\frac{50}{N^2} \]
Si en la primera derivada sustituimos $p_N$ usando la expresión de la curva inversa tenemos: \[ \frac{\mathrm{d} N(p_N)}{\mathrm{d}p_N} = -\frac{50}{\left( \frac{50}{N}\right) ^2 } = \frac{1}{-\frac{50}{N^2} } = \frac{1}{\frac{\mathrm{d} p_N(N)}{\mathrm{d} N}} \]
Hay otra forma alternativa y muy útil de leer la curva inversa de demanda. Para ello debemos tener presente que la función de demanda, de la que obtenemos la curva de demanda, es el resultado de la decisión maximizadora del consumidor.
Supongamos que la curva de demanda fuera* Aunque dice la curva de demanda, la expresión que nos dan es la de la inversa. Como hemos visto, en realidad ambas expresiones, directa o inversa, corresponden a la misma curva. Son dos formas alternativas de escribirla y muchas veces se habla de la curva para referirse a cualquiera de las dos (siempre podemos obtener una de la otra). \[ p_1(x_1) = \frac{100}{x_1} \] Por sencillez vamos a suponer, en este ejemplo, que el bien 1 sólo puede comprarse en unidades enteras.
Si queremos que el consumidor compre 10 unidades tendríamos que proponerle un precio $p_1(10) = \frac{100}{10} = 10$.
Si el precio sube a $p_1'=11$ el consumidor dejaría de comprar la décima unidad, pero seguiría comprando las otras nueve. ¿Por qué?
Dado que la compra es un acto voluntario debemos entender que esa última unidad valía para él las diez libras que pagaba, pero eso era lo máximo que estaba dispuesto a pagar por ella. Si le piden más ya no le interesa comprarla. Si volvemos a subir el precio hasta $p_1'' = 12$ dejaría de comprar también la novena... Podemos concluir que mientras valoraba la décima en 10, por la novena está dispuesto a pagar 11, pero no más. ¿Cuánto valdría para él la segunda unidad? Sol.
Generalizando el razonamiento, supongamos una curva inversa de demanda \[ p_1 = p_1(x_1) \]
Para una cierta cantidad de bien 1, $x_1^0$, tenemos que \[ p_1^0 = p_1(x_1^0) \]
La lectura habitual sería que $p_1^0$ es el precio al que el consumidor demandaría $x_1^0$ unidades del bien.
La nueva lectura es que el consumidor valora la unidad número $x_1^0$ del bien en $p_1^0$ libras. A un precio mayor no compraría esa unidad, aunque sí las anteriores. Cada unidad tiene para él un valor diferente (que es lo máximo que está dispuesto a pagar por ella). Cuando vaya al mercado y vea el precio vigente comprará todas las unidades que, desde su punto de vista, valgan al menos tanto como el mercado pide por ellas.
Ejemplo
Hemos visto anteriormente que la curva de demanda de caramelos de Mary era $C=\frac{120}{4+p_C}$ (cuando $m=120$ y $p_N=4$). La curva inversa de demanda era \[ p_C = \frac{120 - 4 C}{C} \]
Aunque todas las unidades son iguales, la pendiente negativa de la curva de demanda indica que el consumidor valora (está dispuesto a pagar) menos por cada nueva unidad del bien. Nos hacemos ahora una nueva pregunta:
¿Cuánto estaría dispuesto a pagar el consumidor por cierta cantidad de bien 1? Sol.
Aunque la pregunta sea distinta a la anterior podemos responderla con lo que hemos visto antes. ¿cuánto estaría dispuesto a pagar por tres unidades? Si la curva inversa de demanda nos dijera que está dispuesto a pagar 10 por la primera, 8 por la segunda y 7 por la tercera, podríamos concluir que está dispuesto a pagar $10+8+7=25$ en total por las tres.
Veamos un ejemplo en que, además de desarrollar la idea con un poco más de detalle, buscaremos su representación gráfica.
Ejemplo
Llamamos Excedente Bruto, $\mathrm{EB}(x)$, a la función que calcula la máxima cantidad de dinero que el consumidor estaría dispuesto a pagar por $x$ unidades del bien. (Se conoce también como la Disposición Total a Pagar.)
Sería el resultado de agregar la disposición a pagar por cada una de las unidades, mostradas por la curva inversa de demanda.
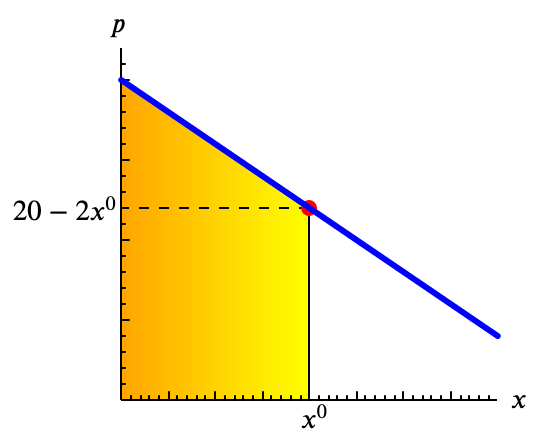
Gráficamente, el Excedente Bruto para una cantidad $x^0$ puede verse como el área bajo la curva de demanda entre 0 y $x^0$.
El área que queda bajo una curva puede calcularse como la integral de la función. Podemos pues expresar el Excedente Bruto como la integral de la curva inversa Cuando decimos que la integral nos da el área de debajo de la función se entiende que la función está representada en la forma habitual, con la variable dependiente en el eje vertical. Como al representar la curva de demanda ponemos en el eje vertical el precio para calcular el área por debajo de la curva, tenemos que integrar la curva expresada en su forma inversa. de demanda \[ \mathrm{EB}(x^0) = \int_0^{x^0} p(x) \mathrm{d}x \]
¿Cómo calcular el Excedente Bruto para una curva concreta?
Si la curva es como la de la figura, el cálculo puede ser complejo (para calcular el área bajo una curva se usa el cálculo integral). En la práctica, al menos en ejemplos y ejercicios, suelen usarse curvas de demanda que son rectas, (como en el anterior ejemplo). En ese caso el área bajo la curva puede descomponerse en un triángulo y un rectángulo, y así es fácil calcular sus áreas.
Usando la función del ejemplo, \[ p=20 - 2 \cdot x \]
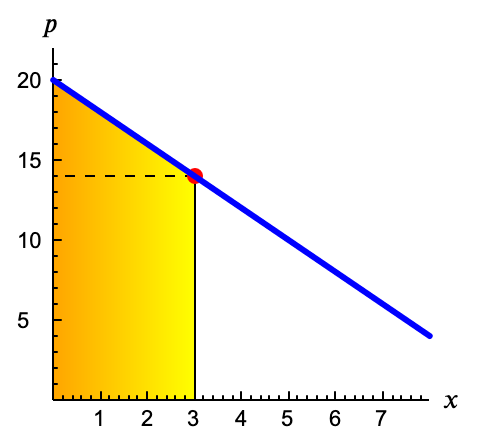
Podemos aplicar la misma lógica que antes utilizando la siguiente figura.
El triángulo tendrá ahora un área \[ \frac{x \cdot (20 - (20-2x))}{2} = \frac{2 \cdot x^2}{2} = x^2 \]
Y el rectángulo \[ x \cdot (20-2x) = 20 x - 2x^2 \]
Agregando las dos áreas \[ \mathrm{EB}(x) = x^2 + 20x -2x^2 = 20 x-x^2 \]
Utilizando la función obtenida podemos comprobar el resultado anterior: \[ \mathrm{EB}(3) = 20 \cdot 3 - 3^2 = 51\]
Si hacemos la integral de la curva de demanda tenemos \[ \int (20 - 2x) \mathrm{d}x = 20 x - x^2 +k \]
Al integrar entre 0 y $x^0$ tenemos \[ \mathrm{EB}(x^0) = \int_0^{x^0} (20-2x) \mathrm{d}x = 20 x^0- (x^0)^2 \] que es el mismo resultado obtenido arriba.
La ventaja de este método es que si tenemos una curva de demanda curvada, la integral sigue funcionando, pero no tenemos el atajo del triángulo y el rectángulo.
Ejemplo
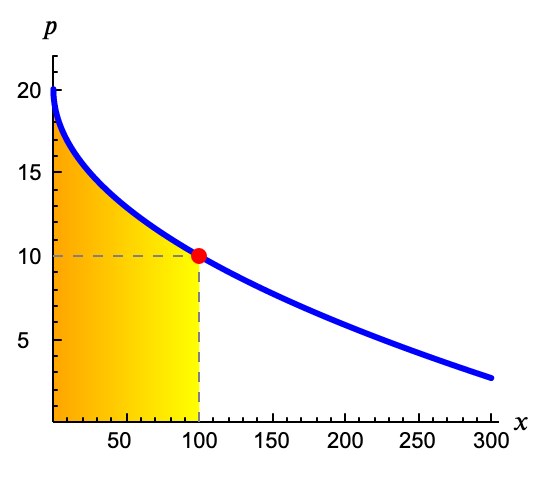
¿Cuál será el Excedente Bruto? El área sombreada tiene un lado curvo, por lo que no podemos usar la geometría. Usamos la integral. \[ \mathrm{EB}(x^0) = \int_0^{x^0} (20-\sqrt{x}) \mathrm{d}x = 20 x^0- \frac{2}{3}x^{3/2} \]
Por ejemplo, si $x=100$ \[ \mathrm{EB}(100) = 2000 - \frac{2}{3} 100^{3/2} = \frac{4000}{3}\]
¿Por qué va un consumidor al mercado?
La pregunta admite una respuesta simple y directa:
Porque le conviene.
¿Podemos desarrollar más esa conveniencia?
EjemploLlamamos Excedente del Consumidor, $\mathrm{EN}(x)$, a lo que el consumidor sale ganando al comprar $x$ unidades del bien, frente a la alternativa de no comprarlas.
El consumidor tiene una disponibilidad a pagar diferente por cada unidad del bien (que podemos calcular usando la curva inversa de demanda). Pero el mercado anuncia un precio que es el mismo para todas las unidades.
El consumidor comprará aquellas unidades que él valora en más de lo que pide el mercado, y sale ganando la diferencia entre lo que hubiera estado dispuesto a pagar y lo que efectivamente ha pagado.
\[ \mathrm{EN}(x) = \mathrm{EB}(x) - p\cdot x\]
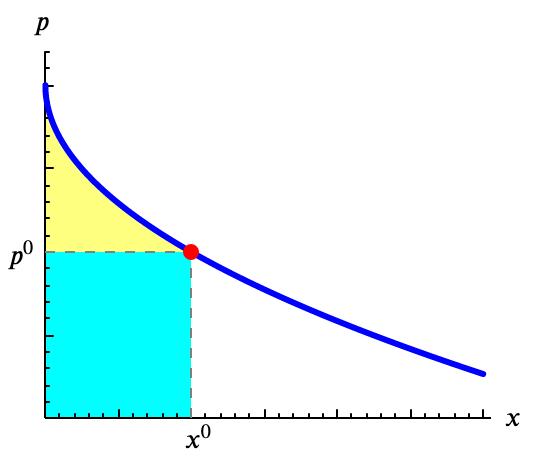
Gráficamente, hemos visto que $\mathrm{EB}(x)$ es el área bajo la curva de demanda (toda el área coloreada), y lo que paga, $p\cdot x$ es el rectángulo azul. La diferencia entre las dos áreas, que es el triángulo amarillo, será el excedente del consumidor.
¿Cómo calculamos el excedente sel consumidor?
Si tenemos calculado el Excedente Bruto es trivial, pues sólo hay que restar $p\cdot x$.
Si no tenemos $\mathrm{EB}(x)$, pero la demanda es una línea recta el excedente del consumidor es el área triangular, que es fácil de calcular.
Si la demanda es una curva no habría más remedio que acudir al cálculo de la integral para obtener el Excedente Bruto.
Ejemplo
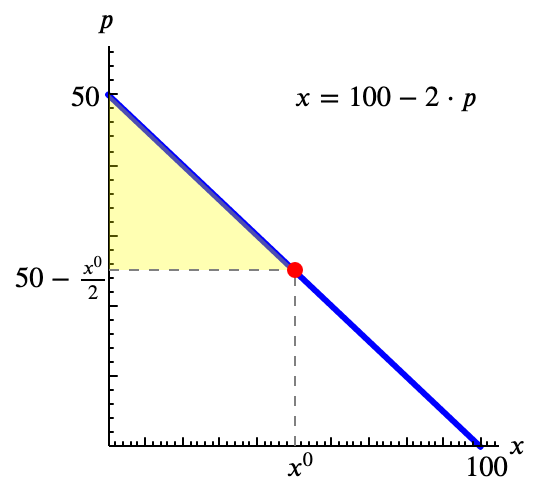
Dado un precio $p^0$ al que el consumidor demanda $x^0 = x(p^0)$, el Excedente del Consumidor puede definirse utilizando la integral como \[ \mathrm{EN}(x^0) = \mathrm{EB}(x^0) - p^0 \cdot x^0 = \int_0^{x^0} p(x) \mathrm{d}x - p^0 \cdot x^0 \]
Pero también podemos plantearlo de otra manera. El área amarilla puede verse como el área que queda a la izquierda de la curva de demanda y por encima de $p^0$.
Esa área puede calcularse haciendo la integral de la curva directa de demanda.* Si no ves esto claro supón que ponemos los ejes al revés (precio en horizontales y cantidad en verticales). Ahora el área amarilla sería lo que está por debajo de la curva desde $p^0$ hacia la derecha, y la calcularíamos con la integral de $x(p)$. \[ \mathrm{EN}(p^0) = \int_{p^0}^{\bar{p}} x(p) \mathrm{d}p \] donde $\bar{p}$ sería el valor de $p$ en el corte de la curva de demanda con el eje vertical.* Hay casos en que usamos curvas de demanda que no llegan a cortar el eje, lo que daría un problema de existencia del excedente (tambien del Excedente Bruto). Pero eso no es un problema demasiado importante, como veremos.
Ahora estaríamos expresando el excedente del consumidor en función del precio, lo que de hecho es más coherente. Antes lo escribíamos en función de $x$, pero esa $x$ era la correspondiente al precio según la curva de demanda.
Ejemplo
Supongamos una situación inicial, en la que el consumidor está consumiendo cierta cantidad de bien $x$, de acuerdo con su curva de demanda.
¿Cómo afectaría al consumidor una subida del precio del bien?
La curva de demanda nos dirá cuánto cambia la cantidad consumida del bien. Hemos estudiado anteriormente esta respuesta, pero ahora nos centramos en un aspecto de la pregunta que tenemos menos trabajado. Formulamos la pregunta de otra forma, para que quede más claro lo que queremos analizar.
¿Cuanto perjudica al consumidor la subida del precio?
Y aquí el Excedente del Consumidor puede ayudarnos a responder. Mira la figura, en la que aparecen tanto el precio inicial como el final. Puedes elegir si ver el EN antes de la subida del precio o después. ¿Cuál es la diferencia?
Si antes de la subida del precio tenía el excedente azul, y después el amarillo, está claro que la subida del precio le ha perjudicado, pues le hace perder una parte de su excedente inicial. Y la diferencia entre ambas áreas nos da una medida del perjuicio sufrido.
La Variación del Excedente del Consumidor es lo que cambia el valor del excedente ante una variación en el precio del bien desde $p^0$ hasta $p^1$.
\[ \Delta \mathrm{EN} = \mathrm{EN}(p^1) - \mathrm{EN}(p^0)\] El cálculo de la variación del excedente presenta las mismas posibilidades que el del excedente.Si tenemos la función $\mathrm{EN}(p)$ calcular la variación no es más que hacer una resta.
Si no tenemos la función pero la demanda es una recta podemos descomponer el área de la variación en un rectángulo y un triángulo y calcular sus áreas fácilmente.
Si la curva de demanda es realmente curva de nuevo haría falta integrar.
Ejemplo
Seguiremos trabajando con la función $ x= 100 - 2 \cdot p$. ¿Cuál sería la variación del excedente del consumidor si el precio pasa de un valor inicial $p^0=15$ a un valor final $p^1=20$ ?
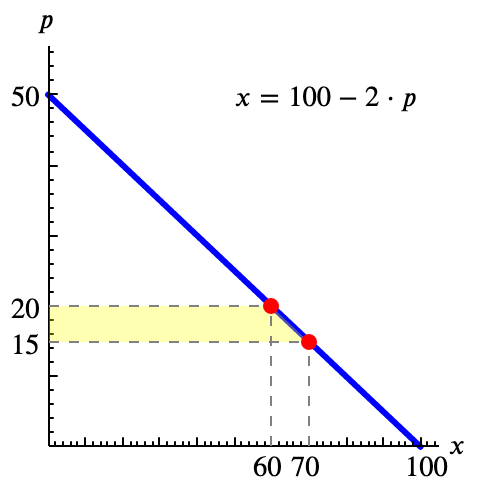
Usamos la función calculada inicialmente, en función de la cantidad del bien, $\mathrm{EN}(x) = \frac{x^2}{4}$
La curva de demanda nos permite calcular las cantidades demandadas antes y después del cambio de precio, $x(15) = 70$ y $x(20) = 60$. Ya podemos calcular la variación de excedente: \[ \Delta \mathrm{EN} = \frac{60^2}{4} - \frac{70^2}{4} = 900 - 1225 = -325 \]
Si hubiéramos usado directamente la función de EN dependiendo del precio, $\mathrm{EN}(p) = p^2 - 100p+2500$, tendríamos \[ \Delta \mathrm{EN} = 20^2- 100\cdot 20 + 2500 - (15^2 - 100\cdot 15 + 2500) = -325 \]
También podríamos haber usado la figura. El área a calcular es la suma del rectángulo y el triángulo. \[ 60\cdot (20-15) + \frac{(70-60)(20-15)}{2} = 325 \]
Observa que en este caso debemos interpretar nosotros sobre la figura que el área es lo que el consumidor pierde, y por eso al resultado obtenido le pondríamos el signo negativo. \[ \Delta \mathrm{EN} = - 325 \]Si estamos dispuestos a usar las integrales, la figura nos muestra que la variación del excedente del consumidor corresponde al área a la izquierda de la curva de demanda entre el precio inicial y el final. Podemos obtener ese área integrando la curva (directa) de demanda entre esos precios. \[ \Delta \mathrm{EN} = - \int_{p^0}^{p^1} x(p) \mathrm{d}p\]
Como antes al calcular el área gráficamente, el signo negativo nos dice que el área al subir el precio es lo que el consumidor pierde (variación negativa en EN).* Matemáticamente se puede obtener, aunque es un poco largo: \[ \Delta \mathrm{EN} = \mathrm{EN}(p^1) - \mathrm{EN}(p^0) = \int_{p^1}^{\bar{p}} x(p) \mathrm{d}p- \int_{p^1}^{\bar{p}} x(p) \mathrm{d}p = \] \[ = \left.\int x(p) \mathrm{d}p \right|_{\bar{p}} - \left. \int x(p) \mathrm{d}p \right|_{p^1} - \left[ \left.\int x(p) \mathrm{d}p \right|_{\bar{p}} - \left.\int x(p) \mathrm{d}p \right|_{p^0} \right] = \] \[ = \left.\int x(p) \mathrm{d}p \right|_{p^0} - \left.\int x(p) \mathrm{d}p \right|_{p^1} = \] \[ = \int_{p^1}^{p^0} x(p) \mathrm{d}p = - \int_{p^0}^{p^1} x(p) \mathrm{d}p \]
Ejemplo
La variación del excedente del consumidor intenta medir el impacto de la subida del precio sobre el bienestar del consumidor.
La palabra bienestar es nueva para nosotros. Hemos hablado de preferencias, de utilidad o de satisfacción. Pero también hemos dicho que esos conceptos eran subjetivos, y no observables ni medibles.
La curva de demanda sí es algo observable a través de las decisiones del consumidor. La variación del excedente resulta ser una herramienta útil.
Es verdad que puede resultar algo simple en términos teóricos. Por ejemplo, no tiene en cuenta los posibles efectos cruzados que el cambio de un precio puede tener sobre el consumo de otros bienes (y sus correspondientes excedentes). Y medir el bienestar en dinero puede resultar engañoso. Las cifras del excedente de un consumidor, aunque sean en dinero, siguen sin ser comparables entre consumidores, pues la valoración del dinero también es subjetiva. ¿Una libra vale lo mismo para cualquier persona? Incluso, para una misma persona, vale lo mismo una libra si tiene 100 que si tiene cien mil?
Pero frente a otras herramientas teóricamente más robustas, el EN tiene la ventaja de ser calculable con relativa facilidad. Y puede considerarse que siempre es mejor tener una herramienta, aunque sea poco precisa, que no tener ninguna. Aunque también es importante ser consciente de esas carencias para no atribuirle más valor del que tiene.
Matemáticamente la obtenemos al sustituir esos valores fijos de $m$ y $p_2$: \[ x_1(p_1) = x_1(p_1, p_2^0, m^0) \]
El excedente del consumidor puede verse también como el área a la izquierda de la curva de demanda y por encima de $p$.
Gráficamente puede verse como el área a la izquierda de la curva de demanda entre el precio inicial y el final.
Curva de demanda
Desplazamientos de la demanda
Curva inversa de demanda
Excedente Bruto (EB)
Excedente neto del consumidor (EN)
Variaciones del excedente neto $(\Delta\textrm{EN})$