Como ejercicio de aplicación de lo anterior, ¿puedes calcular qué cesta de bienes permitiría a Michael obtener una utilidad $u=10$ si los precios son $p_1=4$ y $p_2=9$?
La función de utilidad de Michael es \[ \mathrm{U}(x_1, x_2) = \frac{x_1 \cdot x_2}{x_1 + x_2} \]
- El primer paso sería calcular la relación marginal de sustitución. Sol.
Habrá que calcular las utilidades marginales, y después el cociente. \[ \mathrm{UMg}_1(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} =\frac{x_2 (x_1 + x_2)- x_1 x_2}{(x_1 + x_2)^2} = \frac{x_2^2}{(x_1 + x_2)^2}\] \[ \mathrm{UMg}_2(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} =\frac{x_1 (x_1 + x_2)- x_1 x_2}{(x_1 + x_2)^2} = \frac{x_1^2}{(x_1 + x_2)^2}\] \[ \mathrm{RMS}(x_1, x_2) = -\frac{\mathrm{UMg}_1(x_1, x_2)}{\mathrm{UMg}_2(x_1, x_2)} = -\frac{x_2^2}{x_1^2}\]
- Con la $\textrm{RMS}$ y los precios puedes plantear la condición de tangencia. Sol.
\[\mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \Longrightarrow -\frac{x_2^2}{x_1^2} = -\frac{4}{9}\]
- El punto que buscamos pertenece a la curva de indiferencia 10. Consturye la ecuación de esa curva. Sol.
\[\frac{x_1 \cdot x_2}{x_1 + x_2} = 10 \]
Ya podemos formar el sistema de ecuaciones, que queda \[ \left. \begin{array}{c} -\frac{x_2^2}{x_1^2} = -\frac{4}{9} \\ \\ \frac{x_1 \cdot x_2}{x_1 + x_2} = 10 \end{array} \right\} \]
Resuelve el sistema.Sol.
De la primera ecuación tenemos
\[ -\frac{x_2^2}{x_1^2} = -\frac{4}{9} \Longrightarrow -\frac{x_2}{x_1} = -\frac{2}{3} \Longrightarrow x_2 = \frac{2}{3} x_1 \]
Sustituyendo $x_2$ en la segunda
\[ \frac{x_1 \cdot \frac{2}{3} x_1}{x_1+ \frac{2}{3} x_1} = 10 \]
Simplificamos y resolvemos
\[ \frac{ \frac{2}{3} \cdot x_1^2}{\frac{5}{3} \cdot x_1} = \frac{2 x_1}{5} \longrightarrow \frac{2 x_1}{5}=10 \Longrightarrow \begin{array}{c} x_1^h=25 \\ x_2^h = \frac{50}{3} \end{array}\]
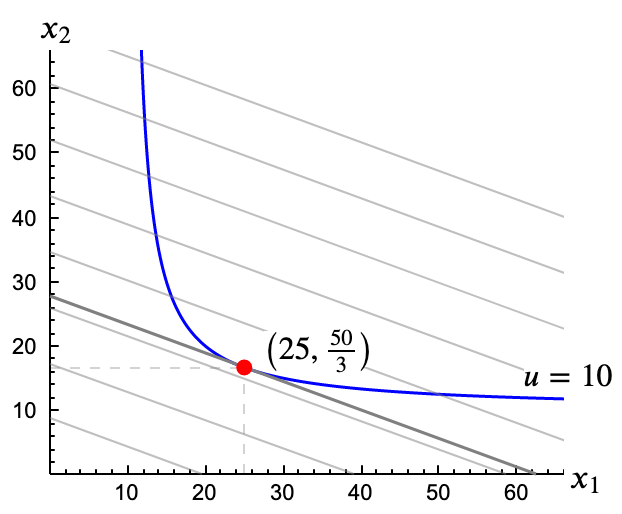
- ¿Cómo será la representación gráfica? (Descríbela con palabras) Sol.
Tenemos un mapa de isocostes formado por rectas con pendiente $-4/9$. Una de ellas es tangente a la curva de indiferencia 10, en el punto $(25, \frac{50}{3})$.
- ¿Cuánto cuesta la cesta óptima?Sol.
$4\cdot 25 + 9 \cdot \frac{50}{3} = 250$