Mary siempre come un caramelo con cada nube, y desecha el posible exceso de cualquiera de los dos. Su función de utilidad es $\mathrm{U}(C, N) =\mathrm{Min}\left\{C, N \right\}$.

En casa Mary consumía 20 caramelos y 20 nubes. El abuelo quiere que Mary tenga la misma utilidad en la isla que en casa. Si los precios son $p_C = 3$ y $p_N = 6$, ¿qué paga tendrá que darle?

• ¿Cuál es la utilidad que tiene que alcanzar Mary? Sol.
  La misma que en casa, que era $\mathrm{Min}\left\{ 20, 20 \right\} = 20$.
• Plantea la ecuación de tangencia. Sol.
  No es posible. Para las preferencias de Mary no es posible sustituir caramelos por nubes. Ella quiere un caramelo con cada nube. Si le quitas un caramelo no puedes sustituirlo por nubes.
• Podemos resolver el problema si no se puede plantear la condición de tangencia? Sol.
  El problema es buscar la cesta más barata que consiga la utilidad 20. La condición de tangencia es una herramienta, que en este caso no funciona. Pero eso no significa que el problema no tenga solución. Habrá que pensar sobre ello.
• Mira la función de utilidad. ¿Qué tiene que pasar para que el resultado sea 20? Sol.
  Que haya 20 caramelos y 20 o más nubes, o bien 20 nubes y 20 o más caramelos.
• ¿Cuál será la combinación más barata de las anteriores? Sol.
  La $(20, 20)$. Todo lo que pase de 20 en sólo uno de los dos bienes sería pagar algo que va a tirar. Si los dos son mayores que 20, la utilidad sería mayor que la buscada.

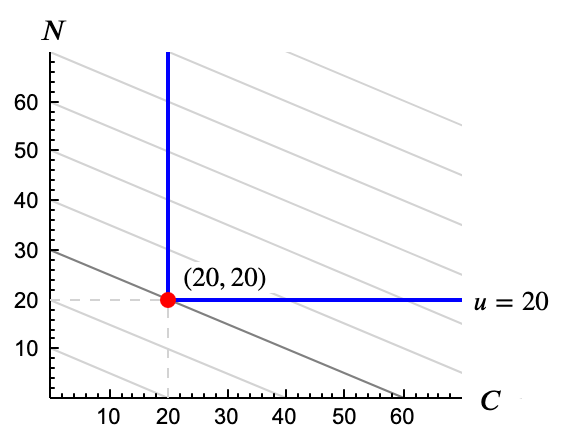
• Vuelve a responder la pregunta, ahora usando la figura. Sol.
  La curva de indiferencia 20 es una línea en L con el vértice en el punto $(20, 20)$. Las líneas isocoste son rectas con pendiente $-1/2$. En los puntos de la parte horizontal de la curva de indiferencia hay caramelos que no se va a comer. Si deja de comprarlos ahorra sin perder utilidad. En la parte vertical sobran nubes. Sólo en el vértice paga lo que necesita nada más. Observa que en los puntos que no son el vértice la isocoste corta a la curva de indiferencia.
• ¿Cuánta paga tendrá que darle el abuelo a Mary?Sol.
  Para comprar la cesta $(20, 20)$ necesita $3\cdot 20 + 6\cdot 20 = 180$ conchas.