Un consumidor tiene preferencias dadas por la función de utilidad \[ \mathrm{U}(x_1, x_2) = x_1 \cdot (x_2 + 20) \]

¿Cuál sería la forma más barata de alcanzar una utilidad $u_1=625$ si los precios son $p_1 = 1$ y $p_2=1$?

• Empieza por calcular la relación marginal de sustitución. Sol.
  Calculamos primero las utilidades marginales \[ \mathrm{UMg}_1(x_1, x_2) = x_2 + 20 \quad \mathrm{UMg}_2(x_1, x_2) = x_1 \] y las usamos para obtener la $\mathrm{RMS}$ \[ \mathrm{RMS}(x_1, x_2) = - \frac{x_2 + 20}{x_1} \]
• ¿Cuál es la ecuación de la curva de indiferencia? Sol.
  $x_1 \cdot (x_2 + 20) = 625$
• Planteamos el sistema formado por la curva de indiferencia y la condición de tangencia \[ \left. \begin{array}{c} x_1 \cdot (x_2 + 20) = 625 \\ - \frac{x_2 + 20}{x_1} = -\frac{1}{1} \end{array} \right\} \]
• ¿Qué conseguimos resolviendo el sistema? Sol.
  Obtenemos el punto que pertenece a la curva de indiferencia y a la recta isocoste más baja posible, que es la tangente a la curva.
  Hazlo. Sol.
  De la segunda ecuación tenemos que $x_2 + 20 = x_1$. Sustituyendo en la primera $x_1^2 = 625 \Longrightarrow x_1^h = 25, \; \; x_2^h=5$.
• ¿Cuánto dinero hace falta? Sol.
  $1 \cdot 25 + 1\cdot 5 = 30$

Repetimos ahora el problema, con los mismos precios pero para alcanzar una utilidad $u_2=200$. ¿Cuál sería la cesta más barata?

Planteamos el nuevo sistema, similar al anterior: \[ \left. \begin{array}{c} x_1 \cdot (x_2 + 20) = 200 \\ - \frac{x_2 + 20}{x_1} = -\frac{1}{1} \end{array} \right\} \]

• ¿Cuál es la solución del sistema? Sol.

  Como antes, de la segunda ecuación tenemos que $x_2 + 20 = x_1$. Sustituyendo en la primera $x_1^2 = 200 \Longrightarrow x_1^h = \sqrt{200} \simeq 14.14$

  Pero ahora $x_2 + 20 = 14.14 \Longrightarrow x_2= -5.86$.

  Una solución negativa para la cantidad de un bien no es aceptable.

  ¿Qué está pasando? Sol.
  Mira la figura.

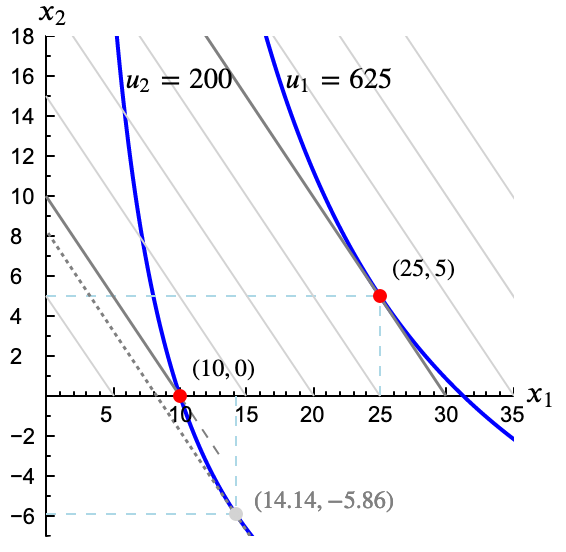
El sistema tiene una solución matemáticamente correcta en $(14.14, -5.86)$. Es el punto donde una isocoste es tangente a la curva de indiferencia 200. Pero esa solución no tiene sentido económico. Nuestro problema tiene unas restricciones implícitas de no negatividad para las cantidades de los bienes. Es más cómodo, aunque formalmente menos riguroso, no hacerlas explícitas hasta que, como en este caso, su existencia se hace notar. ¿Qué hacemos entonces?

Recuerda que el problema es buscar el punto más barato de la curva de indiferencia. Dado que nuestro conjunto de alternativas está formado por la parte de la curva de indiferencia con coordenadas no negativas, la figura nos muestra que el punto más barato es el corte con el eje horizontal. Estamos de nuevo estamos ante una solución de esquina.

En el corte con el eje tenemos $x_2^h=0$ (no se compra nada de bien 2. ¿Cuánto bien 1 habrá que comprar? Sol.

Si la cesta óptima es $(x_1^h, x_2^h) = (10, 0)$, dado que $p_1=1$ para alcanzar la utilidad 200 hace falta un gasto de $1\cdot 10 = 10$.