Volvemos a la isla. Recuerda que los precios vigentes para caramelos y nubes son $p_C=3$ y $p_N=6$

• ¿Puedes calcular lo que costaría una cesta de 10 caramelos y 5 nubes? Sol.
  Basta con usar los precios: $ 3\cdot 10 + 6\cdot 5 = 60$.
  ¿Y la cesta $(6,7)$? Sol.
  Cuesta lo mismo que la anterior: $3\cdot 6+ 6\cdot 7 = 60$.
• ¿Podrías buscar otras cestas que también cuesten 60? (recuerda que aceptamos decimales). ¿Habrá muchas? Sol.
  Hay infinitas. Cualquiera que cumpla la ecuación $3\cdot C + 6\cdot N = 60$. Para cada valor de $C$ (menor que 20) podemos encontrar el correspondiente valor de $N$.
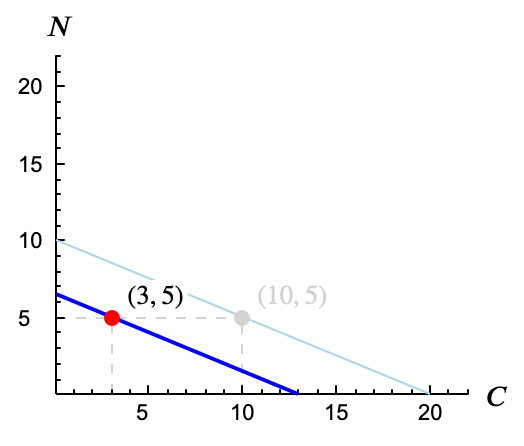
• ¿Y si ponemos en una figura todas las cestas que cuestan 60? Sol.
  Formarán una línea recta. Despejando $N$ en la ecuación, tenemos $N = \frac{60 - 3C}{6}$ que es una recta con corte en ordenadas 10 y pendiente $-3/6 = -0.5$.