El Problema del Consumidor
4.- Sustituyendo un bien por otro
4.- Sustituyendo un bien por otro
Relación marginal de sustitución (Ver en Youtube)

Supongamos un consumidor con preferencias bien comportadas Llamamos preferencias bien comportadas a las que cumplen todas las propiedades propuestas. No sólo son completas y transitivas, sino también continuas, monótonas y convexas. Como veremos, el incumplimiento de alguna de las propiedades tenderá a darnos quebraderos de cabeza. . Como se ha visto anteriormente, pueden ser representadas gráficamente por un mapa de curvas de indiferencia con pendiente negativa, como las de la figura.

Situado inicialmente en un punto (uno cualquiera), un consumidor no tendría inconveniente en moverse a otro que pertenezca a la misma curva de indiferencia. No gana nada, pero tampoco pierde. Dicho de otra forma, aceptaría una reducción en la cantidad de un bien si le compensamos con el suficiente aumento del otro bien. Puedes ver esta idea reflejada en la figura, pero antes de profundizar en ella mira el siguiente ejemplo.

Ejemplo 

Las observaciones del ejemplo nos llevan a construir una nueva herramienta que nos será muy útil en el futuro.

Usaremos la siguiente figura, similar a la del ejemplo pero que nos permite ver diferentes puntos iniciales y variaciones. Puedes elegir la combinación inicial (el punto t) arrastrándolo sobre la figura.* Observa que al mover el punto t siempre se ve resaltada la curva de indiferencia a la que pertenece. No es que la curva se mueva. Por todos los puntos pasa una curva (y sólo una) y se resalta en cada caso la correspondiente al punto que nos interesa. También puedes proponer una variación de $x_1$, positiva o negativa, y automáticamente se mostrará la correspondiente variación de $x_2$ necesaria para mantener al consumidor en un punto indiferente al punto inicial.

La variación total de bien 2 necesaria para compensar la variación de $x_1$ de modo que el consumidor se mantenga en la misma curva de indiferencia.
La relación de sustitución. Es la pendiente del segmento que une el punto inicial y el final. Su valor es la cantidad de $x_2$ necesaria para compensar cada unidad de variación de bien 1.
Relación marginal de sustitución. Es la relación de sustitución (RS), pero para pequeñas variaciones de $x_1$. Gráficamente, es la pendiente de la linea tangente a la curva en el punto t.

Si le das bien 1 ($\Delta x_1 > 0$), habrá que quitarle bien 2 ($\Delta x_2 < 0$) para compensar. Al contrario, si $\Delta x_1 < 0$ (le quitas bien 1), habrá que darle bien 2 ($\Delta x_2 > 0$).

Dado un par de variaciones, $(\Delta x_1, \Delta x_2)$, que mantienen al consumidor indiferente, vamos a llamar relación de sustitución (RS) al cociente $\frac{\Delta x_2}{\Delta x_1}$.

El valor de la relación de sustitución puede ser interpretado como cantidad de bien 2 necesaria para sustituir a una unidad de bien 1 de modo que el consumidor se mantenga con el mismo nivel de satisfacción (utilidad):

\[ \mathrm{RS}(x_1, x_2) = \frac{ \Delta x_2}{ \Delta x_1} \]

En la expresión, RS es una función de $x_1$ y $x_2$ pues, como ya se ha visto en el ejemplo, la cantidad necesaria de bien 2 depende del punto inicial en que nos fijemos.

Example

Si para compensar una reducción de 3 unidades de $x_1$ ($\Delta x_1=-3$) hacen falta 6 unidades de $x_2$ ($\Delta x_2=6$), el cociente sería

\[ \frac{ \Delta x_2}{ \Delta x_1} = \frac{6}{-3} = -2\]

Han hecho falta 2 unidades de $x_2$ por cada unidad de bien $x_1$. El signo negativo nos recuerda que las variaciones tienen signo contrario (aumentamos la cantidad de un bien al reducir la del otro).

Observa la figura. Gráficamente, el cociente de variaciones nos da la pendiente de la recta que pasa por el punto inicial y el final. Moviendo el punto t (punto inicial) podrás ver que la pendiente de esa recta es diferente dependiendo del punto elegido.

Pero además, si desde un mismo punto t probamos diferentes variaciones del bien 1 (puedes proponer diferentes variaciones de $x_1$ usando el deslizador), también obtenemos diferentes rectas, esto es, diferentes valores para $\mathrm{RS}(x_1^\mathbf{t}, x_2^\mathbf{t})$.

Observa lo que pasa si vas probando valores de $\Delta x_1$ cada vez menores (más cercanos a 0, por la derecha o por la izquierda). Verás que si $\Delta x_1$ se va acercando a 0, la recta cuya pendiente calcula RS se va acercando a la recta tangente a la curva en t (la recta que toca a la curva en t sin cortarla). Al valor que toma $\mathrm{RS}(x_1^\mathbf{t}, x_2^\mathbf{t})$ para una variación de $x_1$ muy pequeña lo llamamos relación marginal de sustitución (RMS). La RMS en un punto es pues la pendiente de la recta tangente a la curva de indiferencia en el punto (o, simplemente, la pendiente de la curva en el punto). Eligiendo $\Delta x_1=0$ en la figura, y arrastrando el punto t a donde desees, verás la recta tangente (RMS) en el punto t elegido.

Insistiremos una vez más, porque es importante, en la interpretación. Si en un punto tenemos que $\mathrm{RMS}(x_1^\mathbf{t}, x_2^\mathbf{t}) = -3$, significa que ante una pequeña variación de de $x_1$ haría falta variar $x_2$ en sentido contrario, a razón de 3 unidades de $x_2$ por cada unidad de variación de $x_1$.*

Puesto que la RMS es la pendiente de la recta tangente, la sustitución que indica no es exactamente el movimiento por la curva, sino por dicha recta tangente. Para una variación pequeña esa aproximación es buena, pero si tomamos una variación grande la diferencia puede ser importante. Puedes verlo en la figura.

(Para un punto inicial (1000, 2000), $\Delta x_1=2$ sería una variación pequeña. Pero si el punto inicial es el (4, 3) variar $x_1$ en una unidad sería mucho; el valor de -3 obtenido podría ser apropiado para calcular que $\Delta x_1 = -0.1$ necesitaría una compensación de $\Delta x_2 = 0.3$)

La RMS es la valoración (subjetiva) del consumidor. En cuánto bien 2 valora una unidad de bien 1.

¿Cómo calcular la RMS?

Para que la RMS exista basta con que existan curvas de indiferencia con pendiente negativa, de forma que tenga sentido que la sustitución de cierta cantidad de un bien por el otro deje al consumidor indiferente.*

En el caso de curvas de indiferencia con pendiente positiva (que pueden aparecer si las preferencias no son monótonas), la pendiente de las curvas se calcularía igual (cociente de variaciones) pero la interpretación ya no sería la de una sustitución pues las variaciones no tendrían signo contrario. (En la siguiente página, entre los diversos tipos de preferencias, podrás ver un ejemplo.)

Pero para poder calcular la RMS necesitaríamos tener la función de utilidad correspondiente a las preferencias. Podemos seguir dos caminos distintos. Comenzaremos por el primero, más evidente pero a la larga menos práctico, para después explorar el segundo.

Hemos visto que la RMS es la pendiente de la curva de indiferencia. La función de utilidad nos permite conocer la ecuación correspondiente a la curva de indiferencia que pasa por un punto. Una vez que tenemos la curva expresada como una función conocer la pendiente es inmediato (usando el cálculo) pues la pendiente de una función en un punto es el valor de su derivada.

Ejemplo

Sea la función de utilidad de Peter, que ya fue identificada anteriormente como $\mathrm{U}(x_1, x_2) = x_1 + x_2$ (donde $x_1$ son caramelos y $x_2$ son nubes).

Si nos fijamos en un punto, por ejemplo el (10, 15), tenemos que $U(10, 15) =25$. La curva de indiferencia correspondiente a ese punto será

\[ x_1 + x_2 = 25 \]

Despejamos $x_2$, pues queremos escribirla como una función:

\[ x_2 = 25 - x_1 \]

La expresión obtenida corresponde a una recta con pendiente -1. Y esa pendiente es la RMS. Para Peter una unidad de bien 1 se puede sustituir por una unidad de bien 2.

(Las preferencias de Peter son especialmente sencillas en este sentido, pues siempre valora cada caramelo en una nube. Recuerda las preferencias de Peter cuyas curvas de indiferencia eran rectas, esto es, tenían pendiente constante. No pasará lo mismo con John, como podrás ver en el ejemplo dentro del ShowMath)

En general, dado un punto cualquiera la ecuación de la curva de indiferencia que pasa por él será

\[ \mathrm{U}(x_1, x_2) = u_t \]

donde $u_t$ es el valor de la función de utilidad en el punto inicial t.

De ahí podemos obtener la forma explícita de la curva, despejando $x_2$, lo que dará lugar a una función

\[ x_2 = x_2(x_1; u_t) \]

La derivada de esta función nos dará la RMS para los puntos de la curva $u_t$, que habría que evaluar para $x_1^t$ y así obtener el valor buscado.

\[ \mathrm{RMS}(x_1^t, x_2^t) = \left. \frac{\mathrm{d} x_2(x_1; u_t)}{\mathrm{d} x_1} \right|_{x_1=x_1^t} \]

Ejemplo

La función de utilidad de John era $\mathrm{U}(x_1, x_2) = x_1\cdot x_2$. Si nos fijamos, por ejemplo, en el punto (10, 15) tenemos que $\mathrm{U}(10, 15) = 150$.
La curva de indiferencia es \[ x_1\cdot x_2 = 150 \quad \Longrightarrow \quad x_2 = \frac{150}{x_1} \] Derivando obtenemos la RMS\[ \mathrm{RMS}(x_1; 150) = \frac{\mathrm{d} x_2(x_1; 150)}{\mathrm{d} x_1} = \frac{-150}{x_1^2} \] Y evaluando para $x_1 = 10$ nos queda $\mathrm{RMS}(10, 15) = \frac{- 150}{10^2} = -1.5$
Observa que si tomamos otro punto en la misma curva, como el (30, 5), el valor obtenido para la RMS es diferente.\[ \mathrm{RMS}(30, 5) = \frac{- 150}{30^2} = -\frac{1}{6} \] Esto no debería sorprendernos, pues ya hemos visto que las curvas de indiferencia de John son efectivamente curvas (tienen distinta pendiente en cada punto).

Exploremos ahora el otro camino.

Supongamos una función de utilidad, $\mathrm{U}(x_1, x_2)$, y un punto inicial, $(x_1^t, x_2^t)$. En ese punto la función alcanza un valor, $u_t = \mathrm{U}(x_1^t, x_2^t)$. ¿Cómo cambiaría el valor de la función si le damos al consumidor cierta cantidad adicional de bien 1, digamos $\Delta x_1$, mientras mantenemos constante $x_2$? El valor de la función aumentaría en cierta cuantía, $\Delta u$.*

La variación en la utilidad será la diferencia entre la nueva utilidad, en el punto $(x_1^t+\Delta x_1, x_2^t)$ y la del punto inicial: \[ \Delta u = \mathrm{U}(x_1^t + \Delta x_1, x_2^t) - \mathrm{U}(x_1^t, x_2^t)\]

Llamamos utilidad marginal del bien 1 al cociente $\frac{\Delta u}{\Delta x_1}$, cuya interpretación es lo que aumenta la utilidad por cada unidad de aumento de $x_1$.*

Si $\Delta x_1 < 0$, se dará también que $\Delta u<0$. El cociente seguirá siendo un número positivo. Entendemos que, para pequeñas variaciones, el valor del cociente puede leerse hacia adelante, (aumento de utilidad por unidad de aumento del bien 1) o hacia atrás (pérdida de utilidad por unidad de reducción en el consumo de bien 1).

Por ejemplo, si un aumento de 3 unidades del bien 1 hace crecer el valor de la utilidad en 18, el cociente de variaciones da una utilidad marginal de 6. La utilidad ha aumentado en 6 por cada una de las tres unidades que ha aumentado $x_1$.

Exactamente el mismo razonamiento sirve para definir la utilidad marginal del bien 2.

\[ \mathrm{UMg}_1(x_1, x_2) = \frac{\Delta u}{\Delta x_1} \quad \quad \quad \mathrm{UMg}_2(x_1, x_2) = \frac{\Delta u}{\Delta x_2} \] Antes de generalizar, usaremos el concepto de utilidad marginal dentro del siguiente ejemplo.

Example

Supongamos ahora que sabemos que en el punto t los valores de las utilidades marginales son $\mathrm{UMg}_1(x_1^t, x_2^t) = 6$ y $\mathrm{UMg}_2(x_1^t, x_2^t) = 4$.

¿Cuánto bien 2 haría falta para sustituir (manteniendo la utilidad constante) a una reducción de dos unidades en la cantidad de bien 1 ($\Delta x_1 = -2$)?

Como $\mathrm{UMg}_1(x_1^t, x_2^t) = 6$, la disminución de dos unidades de bien 1 reduciría la utilidad en $(-2)\cdot 6 = -12$. Como una unidad de bien 2 aumenta la utilidad en 4, para recuperar los 12 perdidos harían falta 3 unidades de bien 2. Las utilidades marginales nos han permitido calcular que se puede sustituir 2 unidades de $x_1$ por 3 de $x_2$. Y si planteamos el cociente entre las variaciones, $\frac{\Delta x_2}{\Delta x_1} = \frac{3}{-2} = -1.5$. El cociente es la relación de sustitución, que nos dice que ha hecho falta 1.5 unidades de bien 2 por cada unidad de bien 1 para que el consumidor permanezca indiferente.

Si en un punto $\mathrm{UMg}_1(x_1^t, x_2^t)$ es lo que aumentaría la utilidad por una unidad adicional de bien 1, un aumento de $\Delta x_1$ unidades daría lugar a un aumento total de la utilidad de $ \Delta x_1 \cdot \mathrm{UMg}_1(x_1^t, x_2^t)$. Igualmente, una variación de $x_2$ tendría un efecto sobre la utilidad de $ \Delta x_2 \cdot \mathrm{UMg}_2(x_1^t, x_2^t)$. ¿Qué ocurre si se mueve de un punto a otro de la misma curva de indiferencia? Varían tanto $x_1$ como $x_2$. Cada una de esas dos variaciones tendría su efecto sobre la utilidad, según acabamos de ver. Pero el efecto agregado debe ser nulo, pues termina en un punto indiferente al inicial. Esto permite escribir:

\[ \Delta x_1 \cdot \mathrm{UMg}_1(x_1^t, x_2^t) + \Delta x_2 \cdot \mathrm{UMg}_2(x_1^t, x_2^t) = 0 \] Y reordenando términos llegamos a \[ \frac{\Delta x_2}{\Delta x_1} = -\frac{ \mathrm{UMg}_1(x_1^t, x_2^t)}{ \mathrm{UMg}_2(x_1^t, x_2^t)} \] Este es un resultado importante!! El cociente entre unas variaciones que nos mantienen en la curva es lo que habíamos llamado relación de sustitución. Trabajando con variaciones pequeñas, como se discutió anteriormente, estaríamos hablando de la relación marginal de sustitución. \[ \mathrm{RMS}(x_1, x_2) = -\frac{ \mathrm{UMg}_1(x_1, x_2)}{ \mathrm{UMg}_2(x_1, x_2)} \]

Esta fórmula nos proporciona un método sencillo para calcular la RMS (siempre que conozcamos las utilidades marginales).

Ejemplo

En general, la utilidad marginal puede tener diferente valor dependiendo del punto en que nos fijemos (esto es, es una función que depende de $x_1$ y $x_2$). Pero en las preferencias de Peter ambas utilidades marginales valen 1 en todos los puntos; aumentar $x_1$ en una unidad aumenta la suma en una unidad (y lo mismo pasa con $x_2$).\[ \mathrm{UMg}_1(x_1, x_2) = 1 \quad \quad \quad \mathrm{UMg}_2(x_1, x_2)=1\] Si aplicamos la fórmula obtenida tenemos que \[ \mathrm{RMS}(x_1, x_2) = -\frac{ 1}{ 1} = -1 \] La RMS de Peter es constante, igual a -1 en todos los puntos. Puesto que la RMS es la pendiente de la curva de indiferencia, esto es coherente con las curvas de indiferencia observadas para Peter, que eran rectas con pendiente -1.

Observa además que el resultado es coherente también con lo encontrado anteriormente por el primer camino Obtener la ecuación de la curva de indiferencia que pasa por el punto, derivarla y evaluarla en el punto. .

En una función que depende de más de una variable, la derivada parcial mide el efecto sobre el valor de la función por cada unidad de variación de una de las variables permaneciendo constantes las demás. Esto se adecua perfectamente al concepto de utilidad marginal. Podemos definir las utilidades marginales usando las derivadas parciales de la función U

\[ \mathrm{UMg}_1(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1}\]\[\mathrm{UMg}_2(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \] Como ya se ha hecho antes, dado un punto cualquiera, t, la ecuación de la curva de indiferencia que pasa por él será \[ \mathrm{U}(x_1, x_2) = u_t \] donde $u_t$ es el valor de la función de utilidad en el punto inicial t.

Despejando $x_2$ obtenemos la forma explícita de la curva de indiferencia, $x_2 = x_2(x_1; u_t)$.

Según esta función cada valor de $x_1$ tiene su correspondiente valor de $x_2$ de forma que la utilidad resultante sea $u_t$. Esto puede escribirse como:

\[ \mathrm{U}\left(x_1, x_2(x_1; u_t)\right) = u_t \quad \forall x_1\]Derivando, y teniendo en cuenta que $u_t$ es una constante, tenemos que \[ \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} + \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \cdot \frac{\mathrm{d} x_2(x_1;u_t)}{\mathrm{d} x_1} = 0 \]de donde \[ \frac{\mathrm{d} x_2(x_1;u_t)}{\mathrm{d} x_1} = -\frac{\frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} }{\frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2}} \] Como esto es cierto para cualquier punto inicial, y por tanto para cualquier valor de U, y dadas las definiciones de las utilidades marginales, lo que tenemos es que el cociente de las utilidades marginales (con signo negativo) nos da la función que calcula la RMS en cualquier punto. \[ \mathrm{RMS}(x_1, x_2) = - \frac{\mathrm{UMg}_1(x_1, x_2)}{\mathrm{UMg}_2(x_1, x_2)} \] Fíjate que esto hace este camino más interesante que el anterior, pues en aquél teníamos que recalcular el proceso para cada curva de indiferencia.

Ejemplo

De la función de utilidad de John, $\mathrm{U}(x_1, x_2) = x_1\cdot x_2$, podemos obtener las utilidades marginales \[ \mathrm{UMg}_1(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} = x_2 \quad \quad \mathrm{UMg}_2(x_1, x_2) = \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} = x_1 \] Usando la fórmula obtenida, \[ \mathrm{RMS}(x_1, x_2) = - \frac{\mathrm{MR}_1(x_1, x_2)}{\mathrm{MR}_2(x_1, x_2)} = -\frac{x_2}{x_1} \] (A diferencia del caso de Peter, aquí tanto las utilidades marginales como la relación marginal de sustitución no son constantes, sino funciones que dependen del punto.)

Esta expresión nos da la pendiente de la curva de indiferencia en cualquier punto. Si la usamos para los puntos usados anteriormente, (10, 15) y (30, 5), vemos que se obtiene el mismo resultado que entonces: \[ \mathrm{RMS}(10, 15) = -\frac{15}{10}= -1.5 \quad \quad \mathrm{RMS}(30, 5) = -\frac{5}{30}= -\frac{1}{6} \]

RMS decreciente

Se ha visto que, salvo casos especiales como el de Peter, la RMS de un consumidor depende del punto concreto en que nos fijemos, esto es, las curvas de indiferencia no tienen por qué ser líneas rectas. Probablemente has observado que en los ejemplos propuestos los mapas de indiferencia mostrados están formados por curvas convexas. ¿Tiene esto alguna justificación?

Antes de responder de forma genérica el ejemplo de John puede ayudarnos.

Ejemplo

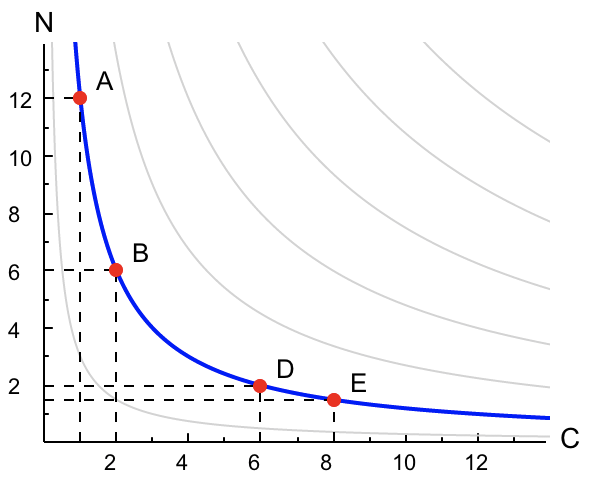
Usamos la misma figura del ejemplo que abría esta página, aunque ahora la leeremos en el otro sentido.

Si John tiene inicialmente la combinación (1, 12), estaría dispuesto a pagar con seis nubes a cambio de un caramelo. En cambio, si estuviera en el punto (6, 2) no estaría dispuesto a pagar más de 0.25 nubes por un caramelo adicional (en realidad lo que vemos es que estaría dispuesto a pagar media nube por dos caramelos). ¿Encuentras justificación para esta diferencia?

Probablemente hayas contestado que sí. En el primer caso sólo tiene un caramelo, y conseguir el segundo estaría muy bien. Además, le pedimos que pague con nubes, de los que tiene bastantes. En cambio en el punto (6, 2) tiene ya bastantes caramelos, y sólo 1.5 nubes. No es raro que esté poco dispuesto a renunciar a nubes (valiosos por su escasez) a cambio de caramelos (que ya tiene unos cuantos).

Recuerda en todo caso que independientemente de que esto nos parezca razonable, otro consumidor podría hacer sus valoraciones con otra lógica.

Si vamos bajando por una curva con pendiente negativa, el valor de $x_2$ va siendo cada vez menor al mismo tiemo que $x_1$ va aumentando. Si además la curva es convexa, conforme bajamos, la pendiente de la curva va siendo cada vez menor (en valor absoluto; la curva baja cada vez más despacio).

La RMS nos dice la cantidad de $x_2$ a la que el consumidor estaría dispuesto a renunciar para conseguir una unidad de $x_1$. Y como hemos visto, gráficamente esa RMS es la pendiente de la curva de indiferencia.

Por tanto, en una curva convexa el consumidor cada vez daría menos $x_2$ para obtener una nueva unidad de $x_1$.

Decir que unas preferencias tienen RMS decreciente es una manera alternativa de decir que las curvas de indiferencias son convexas. * La expresión RMS decreciente es algo informal. En realidad lo que quiere decir es que al bajar por una curva de indiferencia el valor absoluto de la RMS es decreciente.

Como se ha visto en el ejemplo, el decrecimiento de la RMS es algo intuitivamente razonable, pues refleja la idea de que la escasez de un bien lo puede hacer más valioso para el consumidor, mientras que la abundancia haría que se dé menos importancia a una unidad más o menos.

La convexidad de las curvas de indiferencia será pronto una propiedad muy conveniente para nosotros. Los casos en que no se cumpla, como las preferencias de Peter, necesitarán de un tratamiento especial en algunos momentos.

¿Cómo saber si la RMS es decreciente? Si tenemos el mapa, la respuesta es evidente, pues basta mirar la figura para ver si las curvas son convexas.

Si lo que tenemos es la función de utilidad, podríamos usarla para dibujar el mapa, pero también podríamos calcular la RMS y observarla. Por ejemplo, se ha visto que la RMS de John es

\[ \mathrm{RMS}(x_1, x_2) = -\frac{x_2}{x_1} \]

Al bajar por una curva cualquiera, $x_2$ (el numerador) es cada vez menor. Al mismo tiempo, el valor de $x_1$ (el denominador) va aumentando. Por tanto, el valor del cociente es cada vez menor. John cumple con la RMS decreciente (como ya sabíamos por sus curvas).

Transformaciones de la función de utilidad y RMS.

Sabemos que la función de utilidad es una función que pone números a las cestas con el único requisito de poner números mayores a las cestas mejores, y esto hace que unas mismas preferencias puedan ser representadas por más de una función de utilidad.

Diferentes funciones asignarán distinto número a la misma cesta. Pero lo importante es que las cestas que con una función son indiferentes lo sean también con la otra (si no, no estaríamos representando las mismas preferencias).

Los números de una función de utilidad no tienen significado por sí mismos; sólo tienen sentido cuando se comparan entre sí.* La función de utilidad es una función ordinal, no cardinal: ordena, no mide.

Pero las curvas de indiferencia recogen puntos indiferentes, y su pendiente, la RMS, sí tiene un significado real. Si en un punto RMS=-3 significa que en ese punto el consumidor daría (o pediría) 3 unidades de bien 2 por una de bien 1.

Si dos funciones de utilidad representan a las mismas preferencias, deberían dar lugar a la misma RMS en cualquier punto.

Example

Ya hemos visto que si $\mathrm{U}(x_1, x_2)= x_1\cdot x_2$, tenemos que \[ \mathrm{UMg}_1(x_1, x_2) = x_2 \quad \quad \mathrm{UMg}_2(x_1, x_2) = x_1 \] de donde \[ \mathrm{RMS}(x_1, x_2) = -\frac{x_2}{x_1} \] La función $\mathrm{V}(x_1, x_2)=2\cdot x_1\cdot x_2$ asigna a cada punto un número igual al doble del que le asigna la función $\mathrm{U}$. Está claro que si a dos puntos la función les asignaba el mismo número (eran indiferentes), la función $\mathrm{V}$ también les asigna el mismo número (el doble que antes) por lo que según V, también son indiferentes. La ordenación que hace la función $\mathrm{V}$ es exactamente la misma que la que hace $\mathrm{U}$; las dos funciones representan a las mismas preferencias, aunque usen números distintos.

Para calcular la RMS con la función $\mathrm{V}$, tenemos sus utilidades marginales, que son \[ \mathrm{VMg}_1(x_1, x_2) = 2\cdot x_2 \quad \quad \mathrm{VMg}_2(x_1, x_2) = 2\cdot x_1 \] y de ahí \[ \mathrm{RMS}(x_1, x_2) = -\frac{2\cdot x_2}{2\cdot x_1} = -\frac{x_2}{x_1} \] Como era de esperar, la función $\mathrm{V}$ tiene la misma RMS que la función $\mathrm{U}$ en todos los puntos.

Podemos demostrar que cualquier transformación monótona de una función de utilidad tiene la misma RMS que la original.

Sea una $\mathrm{U}(x_1, x_2)$ una función de utilidad, y $f(x)$ una transformación monótona.

Llamamos $\mathrm{V}$ ta la función resultante de aplicar la transformación $f$ a la función $\mathrm{U}$. Al ser $f$ una transformación monótona, $\mathrm{V}(x_1, x_2)$ será una función de utilidad para las mismas preferencias representadas por $\mathrm{U}(x_1, x_2)$. \[ \mathrm{V}(x_1, x_2) = f\left( \mathrm{U}(x_1, x_2)\right)\] Las utilidades marginales de $\mathrm{V}$ serán, usando la regla de la cadena, \[ \mathrm{VMg}_1(x_1, x_2) = \frac{\partial \mathrm{V}(x_1, x_2)}{\partial x_1} = \frac{\mathrm{d} f(U)}{\mathrm{d} U}\cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1} \] \[ \mathrm{VMg}_2(x_1, x_2) = \frac{\partial \mathrm{V}(x_1, x_2)}{\partial x_2} = \frac{\mathrm{d} f(U)}{\mathrm{d} U}\cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2} \] Denotarmos como $ \mathrm{RMS}_V(x_1, x_2) $ a la relación marginal de sustitución obtenida de la función $\mathrm{V}$ \[ \mathrm{RMS}_V(x_1, x_2) = - \frac{\mathrm{VMg}_1(x_1, x_2) }{\mathrm{VMg}_2(x_1, x_2) } = - \frac{\frac{\mathrm{d} f(U)}{\mathrm{d} U}\cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1}}{\frac{\mathrm{d} f(U)}{\mathrm{d} U}\cdot \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2}} = \] \[ \quad \quad \quad = - \frac{ \frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_1}}{\frac{\partial \mathrm{U}(x_1, x_2)}{\partial x_2}} = - \frac{\mathrm{UMg}_1(x_1, x_2) }{\mathrm{UMg}_2(x_1, x_2) } = \mathrm{RMS}_U(x_1, x_2)\] Podemos usar este resultado para saber si dos funciones representan o no a las mismas preferencias (viendo las funciones no siempre es fácil saber si una es transformación de la otra).

Ejemplo 

Y para acabar, un caso diferente. Hemos venido hablando de las preferencias de Peter y de John. Hemos visto sus mapas de indiferencia, las hemos representado con funciones de utilidad y hemos calculado sus respectivas relaciones marginales de sustitución. ¿Y las preferencias de Mary?

Ejemplo 

Resumiendo:

Si en un punto la curva de indiferencia de un consumidor tiene pendiente negativa, es posible sustituir cierta cantidad de un bien por cierta cantidad del otro de manera que el consumidor tenga la misma satisfacción (termine en otro punto de la misma curva).

Relación de sustitución (RS)   Utilidad marginal (UMg)   Recta tangente   Relación marginal de sustitución (RMS)   RMS decreciente

Cuestiones de Autoevaluación




Anterior  Volver  Siguiente