(Concepto matemático)$\quad \quad$
La pendiente de una recta es un número que indica cuanta inclinación tiene (a mayor pendiente más inclinada es una recta).
La pendiente mide cuanto varia la variable dependiente Representada en el eje vertical. por unidad de variación de la variable independiente Representada en el eje horizontal. y es la misma a lo largo de toda la recta.
Gráficamente, para una recta $y(x)$, la pendiente puede calcularse, al pasar de un punto a otro cualquiera de la misma recta, como $\frac{\Delta y}{\Delta x}$.
Ejemplo
En la figura, la recta azul tiene una pendiente de $-2$.
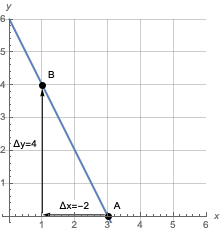
Puedes calcular esta pendiente, por ejemplo, pasando del punto A $=(3,0)$ al B $=(1,4)$, como $\frac{\Delta y}{\Delta x}=\frac{4}{-2}=-2$.
Si las variables cambian en sentido contrario, la pendiente es negativa. Por el contrario, si las variables cambian en el mismo sentido, la pendiente es positiva.
Ejemplo
Tres rectas pasan por $(2,3)$.
Si aumentamos $x$ en una unidad ($x$'$=3$) la variación en $y$ es diferente para cada recta:
- La recta
- La siguiente es la
- Finalmente, la de menos pendiente es la
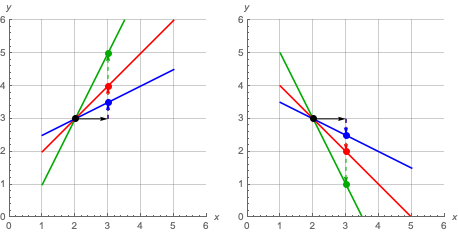
Cada recta en la figura de la izquierda se diferencia de la del correspondiente color en el gráfico de la derecha en el sentido de las variaciones, siendo su pendiente la misma.
Las rectas en la figura de la derecha tienen la misma pendiente pero con signo negativo ($y$ varía en sentido contrario a $x$).