Utilidad marginal (UMg)
La utilidad marginal de un bien es el aumento en la utilidad del consumidor por unidad de aumento en el consumo del bien, manteniendo el consumo del otro bien constante (y suponiendo una variación de $x_1$ pequeña).
Se puede cacular, aproximadamente, mediante el cociente $\frac{Δ\mathrm{U}}{Δx_1}$, aunque la definición formal requiere calcular el límite del cociente para una variación del bien infinitesimal (es decir, la derivada parcial). Muy pequeña (casi 0).
\[\textrm{MU}_1(x_1, x_2) = \frac{∂\mathrm{U}(x_1,x_2)}{∂x_1}\] \[\textrm{MU}_2(x_1, x_2) = \frac{∂\mathrm{U}(x_1,x_2)}{∂x_2}\]Ejemplo
$\mathrm{U}(x_1,x_2)= x_1\cdot x_2$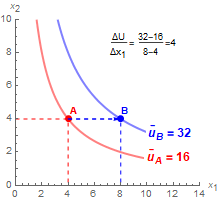 
Empezando en $A=(4,4)$, un aumento de bien 1 de 4 unidades, aumenta la utilidad en $32-16=16$. Así, $\frac{\Delta u}{\Delta x_1}= \frac{16}{4}=4$ es el aumento en utilidad por unidad de aumento en bien 1.
Si en vez de variar el bien 1 en 5 unidades, varía solo un poco (variación cercana a 0), obtenemos la utilidad marginal
\[\frac{\delta \mathrm{U}(x_1,x_2)}{\delta x_1}=4\] cuya lectura es similar:La utilidad aumenta en 4 por unidad de variación del bien $x_1$ (para una pequeña variación del bien 1).