Ejemplo 7: ES y ER de Sandra

Las preferencias de Sandra pertenecen a la familia de las preferencias cuasilineales, y ya vimos que tienen ciertas particularidades, que ahora reaparecerán.

La función de utilidad de Sandra es \[ \mathrm{U}(x_1, x_2) = 5 \cdot \sqrt{x_1} + x_2 \]

Partimos de una situación inicial en la que $m=60$, $p_1=3$ y $p_2=4$, y se produce una subida del precio del bien 1 hasta $p_1'=5$. Queremos calcular el efecto total y descomponerlo en efecto renta y efecto sustitución.

Comenzamos como siempre calculando la demanda inicial, A, y la final, B, lo que nos permitirá obtener el efecto total.
La relación marginal de sustitución es Calculamos las utilidades marginales, \[ \mathrm{UMg}_1(x_1, x_2) = \frac{5}{2 \sqrt{x_1}} \quad \mathrm{UMg}_2(x_1, x_2) = 1 \] y obtenemos la RMS como cociente de ellas. \[ \mathrm{RMS}(x_1, x_2) = - \frac{5}{2 \sqrt{x_1}}\] $\mathrm{RMS}(x_1, x_2) = - \frac{5}{2 \sqrt{x_1}}$* Como ya se vio, en las preferencias cuasilineales la RMS no depende de la cantidad del bien que entra en la función de forma lineal (en este caso $x_2)$. . Podemos construir la ecuación presupuestaria y la de tangencia: \[ \left. \begin{array}{c} 3 x_1 + 4 x_2 = 60 \\ -\frac{5}{2 x_1^2} = -\frac{3}{4} \end{array} \right\} \]
Es un sistema peculiar, en el que la segunda ecuación nos proporciona directamente el valor de $x_1$, y luego la ecuación presupuestaria nos da $x_2$. La solución es el punto A: \[ x_1^A = \frac{100}{9} \quad \quad x_2^A = \frac{20}{3}\] Para obtener el punto B hacemos lo mismo, pero usando el nuevo precio del bien 1: \[ \left. \begin{array}{c} 5 x_1 + 4 x_2 = 60 \\ -\frac{5}{2 x_1^2} = -\frac{5}{4} \end{array} \right\} \] \[ x_1^B = 4 \quad \quad x_2^B = 10 \] Podemos calcular el efecto total para cada bien, \[ ET_1 = x_1^B - x_1^A = 4 - \frac{100}{9} = - \frac{64}{9} \] \[ ET_2 = x_2^B - x_2^A = 10 - \frac{20}{3} = \frac{10}{3} \]
El siguiente paso es calcular el punto C, que sería el punto al que nos llevaría el efecto sustitución al compensar la renta.
Usamos la función de utilidad para calcular su valor en el punto A: \[ \mathrm{U}\left( \frac{100}{9}, \frac{20}{3} \right) = 5 \sqrt{\frac{100}{9}} + \frac{20}{3} = \frac{70}{3} \]

El punto C es la solución al sistema formado por la ecuación de la curva de indiferencia inicial y la condición de tangencia: \[ \left. \begin{array}{c} 5 \cdot \sqrt{x_1} + x_2 = \frac{70}{3} \\ -\frac{5}{2 x_1^2} = -\frac{5}{4} \end{array} \right\} \]

Como en los anteriores, la condición de tangencia nos proporciona el valor de $x_1$, y usamos después la otra ecuación para calcular $x_2$. El resultado es \[ x_1^C = 4 \quad \quad x_2^C = \frac{40}{3} \]
Una vez que tenemos los tres puntos ya podemos calcular los efectos: \[ ES_1 = x_1^C - x_1^A = 4 - \frac{100}{9} = -\frac{64}{9} \] \[ ES_2 = x_2^C - x_2^A = \frac{40}{3} - \frac{20}{3} = \frac{20}{3} \] \[ ER_1 = x_1^B - x_1^C = 4-4 = 0 \] \[ ER_2 = x_2^B - x_2^C = 10 - \frac{40}{3} = - \frac{10}{3} \] \[ ET_1 = x_1^B - x_1^A = 4 - \frac{100}{9} = - \frac{64}{9} \] \[ ET_2 = x_2^B - x_2^A = 10 - \frac{20}{3} = \frac{10}{3} \]

En el resultado obtenido hay una diferencia con otros casos, y es que el efecto renta sobre el bien 1 resulta ser nulo. No es tan raro si tenemos en cuenta que la cantidad óptima de bien 1 sale de la ecuación de tangencia, donde no está la renta. Y el efecto renta es en definitiva la respuesta a un cambio de renta.

En ocasiones se utilizan las preferencias cuasilineales precisamente por esta ausencia de efecto renta (que en realidad es ausencia sólo para el bien 1, no para el bien 2).

Entramos ahora en un segundo aso más complicado. Si vuelves a recordar nuestro estudio de las preferencias de Sandra, vimos que la cantidad de bien 1 no dependía de la renta, siempre y cuando el consumidor tuviera renta suficiente. Por debajo de cierto valor de $m$ la condición de tangencia no funcionaba, y nos encontrábamos con soluciones de esquina, en que el consumidor se gastaba toda su renta en bien 1.

Si nos encontramos con uno de estos casos habrá que estar atentos.

Supongamos que a partir de la misma situación inicial de antes, $m=60$, $p_1=3$ y $p_2=4$, ahora el precio del bien 1 baja hasta $p_1''=1.5$ ¿Cuáles serán los distintos efectos?

El primer paso es calcular los puntos A y B.

El punto A es el mismo que en el caso anterior, por lo que no hace falta volver a calcularlo, \[ x_1^A = \frac{100}{9} \quad \quad x_2^A = \frac{20}{3}\]

Para calcular el punto B comenzamos por plantear el sistema para el nuevo precio \[ \left. \begin{array}{c} \frac{3}{2} x_1 + 4 x_2 = 60 \\ -\frac{5}{2 x_1^2} = -\frac{3/2}{4} \end{array} \right\} \]

Pero al resolver este sistema aparece un problema. La segunda ecuación da como resultado $x_1 = \frac{400}{9}$, pero al sustituir este valor en la segunda aparece $x_2= -\frac{20}{3} $. Y un resultado negativo en la cantidad de un bien no tiene sentido para nosotros.* De hecho lo que ocurre es que la renta no llega para comprar $\frac{400}{9}$ unidades de bien 1. Como ya se ha dicho arriba, nos encontramos ante una solución de esquina. La decisión óptima será gastar toda la renta en bien 1. \[ x_1^B = \frac{60}{3/2} = 40 \quad \quad x_2^B = 0 \]
Para calcular el punto C comenzaríamos por obtener la utilidad en el punto A, cosa que ya hemos hecho arriba obteniendo $\mathrm{U}(\frac{100}{9}, \frac{20}{3}) = \frac{70}{3}$.
Construimos el sistema con la ecuación de la curva de indiferencia y la condición de tangencia \[ \left. \begin{array}{c} 5 \cdot \sqrt{x_1} + x_2 = \frac{70}{3} \\ -\frac{5}{2 x_1^2} = -\frac{3/2}{4} \end{array} \right\} \]

Pero pasa lo mismo que en el anterior; aparece una solución $(x_1, x_2) = (\frac{400}{9}, -10)$ que no resulta aceptable.

Dado que no podemos llegar al punto donde la curva de indiferencia inicial cumpliría la condición de tangencia, la compensación será llevarle al punto más barato de esa curva, que será el corte con de la curva con el eje horizontal.\[ 5 \cdot \sqrt{x_1} + 0= \frac{70}{3} \quad \Longrightarrow \quad x_1 = \frac{196}{9} \]

Esto nos deja el punto C \[ x_1^C = \frac{196}{9} \quad \quad x_2^C = 0 \]
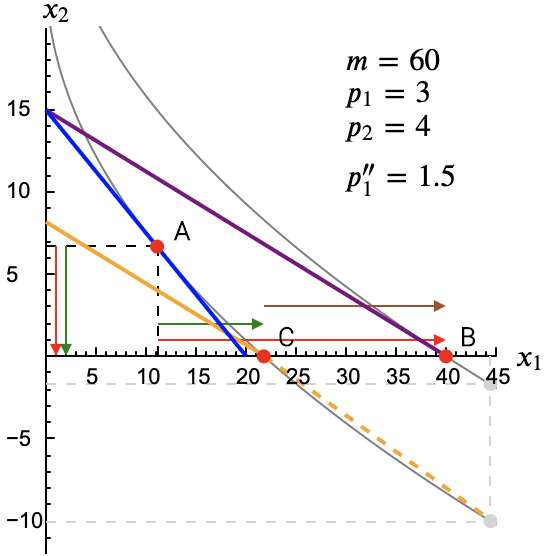
Ya podemos calcular los diferentes efectos mediante las diferencias entre las coordenadas de A, B y C. \[ ES_1 = x_1^C - x_1^A = \frac{196}{9} - \frac{100}{9} = \frac{96}{9} \] \[ ES_2 = x_2^C - x_2^A = 0 - \frac{20}{3} = -\frac{20}{3} \] \[ ER_1 = x_1^B - x_1^C = 40-\frac{196}{9} = \frac{64}{9} \] \[ ER_2 = x_2^B - x_2^C = 0 - 0 = 0 \] \[ ET_1 = x_1^B - x_1^A = 40 - \frac{100}{9} = \frac{260}{9} \] \[ ET_2 = x_2^B - x_2^A = 0 - \frac{20}{3} = -\frac{20}{3} \]

En este caso, al aparecer las soluciones de esquina, encontramos que sí que hay efecto renta sobre el bien 1, y en cambio no lo hay sobre el bien 2.