|
El Problema del Consumidor 2.- Las preferencias |
El problema del consumidor consiste en elegir la mejor opción de entre las que están a su alcance. Hemos recogido esas alternativas mediante el conjunto presupuestario. El siguiente paso es preguntarnos que significa "la mejor", y expresar la respuesta de forma que nos permita avanzar.
Mostremos al consumidor dos cestas distintas, $\mathrm{A}$ y $\mathrm{B}$ (puntos en $\mathbb{R}^2_+$). Al preguntarle sobre ellas nos puede decir que prefiere la cesta $\mathrm{A}$ a la $\mathrm{B}$, a lo que nosotros nos referiremos como $\mathrm{A} \succ \mathrm{B}$, o al revés. También es posible que nos diga que las encuentra igual de buenas: $\mathrm{A} \sim \mathrm{B}$. El proceso se puede repetir tantas veces como queramos con nuevos pares de cestas. Y es muy probable que diferentes consumidores nos responan a la misma cuestión de manera diferente: que te guste una cesta más que otra es algo subjetivo.
Algunos consumidores podrán explicar su método de comparación (por ejemplo, "escojo la cesta que tenga más bien 1", o "escojo la cesta que tenga más cantidad total de ambos bienes"). Otros pueden no saber explicar sus respuestas en cada caso. Por lo general, el término preferencias del consumidor se utiliza para describir lo que un consumidor opina sobre las distintas combinaciones que se le pide que compare. Fíjate que la pregunta es "¿cuál preferirías consumir?": no importa si la cesta es alcanzable o no.*
El planteamiento de las preferencias del consumidor puede expresarse matemáticamente mediante la teoría de las relaciones binarias. Este campo no se trata aquí en profundidad, pero utilizaremos su lenguaje para expresar las propiedades que se piden a las preferencias del consumidor con las que vamos a trabajar.
Para representar las preferencias de un consumidor utilizamos la relación de preferencia débil $\succcurlyeq$.
Dadas dos cestas, $\mathrm{A}$ y $\mathrm{B}$, decimos que $\mathrm{A}$ es débilmente preferida a $\mathrm{B}$, $\mathrm{A} \succcurlyeq \mathrm{B}$, si el consumidor piensa que la combinación $\mathrm{A}$ es al menos tan buena (no peor) como la combinación $\mathrm{B}$.
Utilizamos la preferencia débil para definir otras dos relaciones:
Escribiremos $\mathrm{A} \succ \mathrm{B}$ para denotar que la cesta $\mathrm{A}$ es preferida a la cesta $\mathrm{B}$, y si el consumidor está indiferente entre dos cestas, lo denotamos con $\mathrm{A} \sim \mathrm{B}$.
Como hemos hecho antes con la restricción presupuestaria, nuestro objetivo será representar esas preferencias del consumidor, primero gráficamente, y después en expresión matemática.
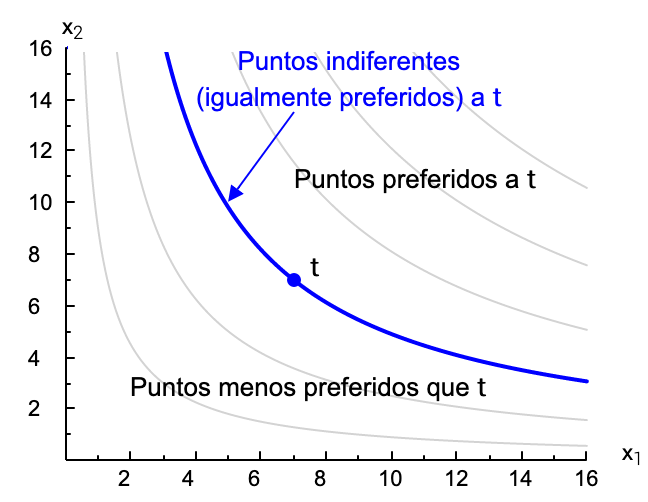
Para mostrar las preferencias del consumidor en un gráfico, cogemos un punto y pedimos al consumidor que nos muestre otros que le gusten lo mismo (es decir, puntos entre los cuales está "indiferente"). Uniendo todos esos puntos obtenemos una línea que contiene los puntos que para el consumidor son indiferentes al punto inicial (y, por tanto, indiferentes también entre ellos), a la cual nos referimos como curva de indiferencia.* Puedes ver en la figura la curva de indiferencia del punto t. A un lado de la curva (normalmente en la parte superior) estarán los puntos mejores al inicial, es decir los puntos preferidos. Al otro lado estarán los puntos peores. Repitiendo el proceso para diferentes puntos de partida podemos obtener las diferentes curvas de indiferencia. El conjunto de todas estas curvas se denomina el mapa de indiferencia.
Cada consumidor puede tener preferencias (y, por tanto, curvas de indiferencia) diferentes a las de los demás. Sin embargo, supondremos que las preferencias de los consumidores cumplen ciertos requisitos. Algunas de estas propiedades son necesarias para construir la teoría, mientras que otras simplemente nos facilitan el trabajo. En cualquier caso, las propiedades que se asumen sobre las preferencias de los consumidores no son demasiado exigentes y están dentro de lo razonable.
Las preferencias deben cumplir la completitud: no tiene sentido buscar la mejor cesta si algunas no pueden compararse. En todo caso la indiferencia entre cestas es posible, por lo que suponer preferencias completas no parece pedir mucho.
Un consumidor tiene preferencias completas si su relación de preferencia débil es completa (se puede utilizar para cualquier par de cestas): \[ \forall \mathrm{A}, \mathrm{B} \in \mathbb{R}^+_2 \quad \mathrm{A} \succcurlyeq \mathrm{B} \quad \mathrm{o} \quad \mathrm{B} \succcurlyeq \mathrm{A} \quad \mathrm{o} \mathrm{\quad ambas} \]
¿Serán las relaciones binarias $\succ$ (preferencia estricta) y $\sim$ (indiferencia) completas?*
Las preferencias son transitivas si siempre que la primera cesta es al menos tan buena como la segunda y la segunda a la tercera, la primera es también preferida a la tercera.
$\forall \mathrm{A}, \mathrm{B}, \mathrm{C} \in \mathbb{R}^+_2,$ $\quad \mathrm{A} \succcurlyeq \mathrm{B} \quad \mathrm{y} \quad \mathrm{B} \succcurlyeq \mathrm{C} \quad \Longrightarrow \mathrm{A} \succcurlyeq \mathrm{C} $
La transitividad de la preferencia débil resulta en la transitividad tanto de la preferencia estrica como de la indiferencia.*
Observa que la causalidad funciona únicamente en una dirección: si la cesta tiene más de ambos bienes entonces es preferida, pero la implicación puede no ser cierta en el otro sentido. Por ejemplo, una cesta podría ser preferida a otra que tuviera más de un bien y menos del otro (en la última figura de esta sección, el punto $\mathrm{y}$ es preferido al $\mathrm{z}$).
Podría pensarse que siempre habrá un punto en el que el consumidor se "sacie" al consumir, y puede que no quiera más cantidad de bienes aunque se la regalen. Pero los problemas en que estamos interesados son normalmente situaciones en las que tal nivel de saciedad está más allá de las posibilidades económicas del consumidor, y por tanto la monotonicidad es un supuesto razonable a efectos prácticos.
Se dice que las preferencias del consumidor son monótonas si al aumentar las cantidades de ambos bienes resulta siempre una cesta mejor que la inicial: \[ (x_1, x_2) > (y_1, y_2) \quad \Longrightarrow \quad (x_1, x_2) \succ (y_1, y_2) \]
Fíjate que usamos dos símbolos diferentes, primero el símbolo "mayor que..." (para comparar coordenadas de vectores, que son números) y después el símbolo "preferido a..." (que es la relación de preferencia sobre cestas).
Si aumentar la cantidad de uno de los bienes (sin reducir la del otro) garantiza que el consumidor mejora, hablamos de monotonicidad fuerte.
Se pueden distinguir dos grados de convexidad.
Las preferencias del consumidor son convexas si para cualquier par de cestas ente las que el consumidor está indiferente, toda combinación lineal convexa de ambas es débilmente preferida (hablando en términos gráficos, dadas dos cestas indiferentes todos los puntos del segmento de recta que une esas dos cestas son débilmente preferidos a ellas).
$ (x_1, x_2) \sim (y_1, y_2) \quad \Longrightarrow$ $\quad \lambda \cdot (x_1, x_2) + (1-\lambda ) \cdot (y_1, y_2) \succcurlyeq (x_1, x_2)$ $ \quad \forall \lambda \in (0, 1) $Si sustituimos en la expresión anterior la preferencia débil con la estricta, $\succ$, tendríamos preferencias estrictamente convexas. Si hay puntos en el segmento que son indiferentes a los extremos, hablaríamos de convexidad no estricta.
En muchos casos, el término convexidad se usa para referirnos a la convexidad estricta. Es una relajación en el lenguaje que puede ser aceptable en términos informales pero se debería evitar si queremos ser precisos. Por lo que veremos enseguida, algunas cosas funcionan de diferente manera cuando se da la convexidad estricta y cuando no.
Como se ha dicho ya, distintos consumidores pueden tener distintas preferencias, lo que dará lugar a diferentes mapas de indiferencia. Pero las propiedades anteriores nos permiten decir algunas cosas con carácter general:
Dado un punto de partida (cualquiera), habrá unos puntos mejores y otros peores que él. La continuidad nos asegura que entre los puntos mejores y los peores debe haber una frontera formada por puntos indiferentes, ya que si no estaríamos saltando de una satisfacción mayor a una menor sin pasar por una igual a la inicial. Para que esa frontera realmente separe puntos preferidos de puntos despreferidos no puede dejar huecos, es decir, cada punto debe estar tocando a otros indiferentes a él.*
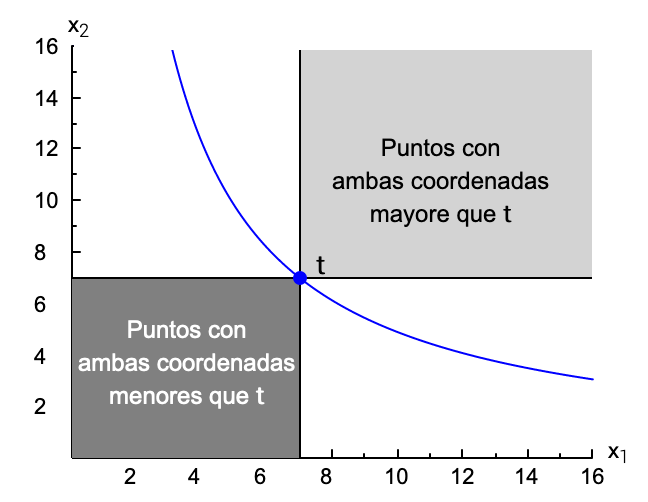
Dada la monotonía, los puntos indiferentes entre sí no pueden formar una superficie, pues cualquier superficie contiene forzosamente puntos con las dos coordenadas mayores que otros, que por la monotonicidad serían preferidos, no indiferentes. En consecuencia los puntos indiferentes deben formar líneas. Llamaremos a esas líneas curvas de indiferencia (de hecho ya lo hemos hecho más arriba).
La monotonicidad garantiza también que dichas líneas no pueden tener pendiente positiva, pues en ese caso habría en la línea puntos con ambas coordenadas mayores que otros.
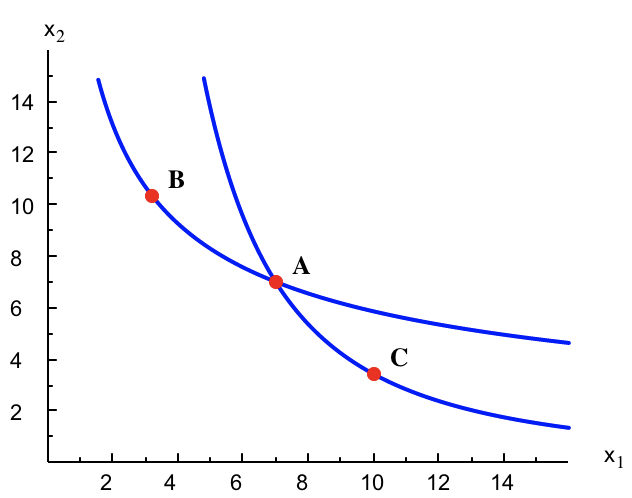
Además, dos curvas de indiferencia no pueden cortarse, ya que si entre dos curvas hay un punto de corte, $A$ en la figura, este debería ser indiferente a los de ambas curvas, como $B$ y $C$. Pero entonces la transitividad permitiría afirmar que $B$ y $C$ serían indiferentes, lo que contradice el que pertenezcan a curvas distintas.
En definitiva, unas preferencias monótonas y continuas* se pueden representar gráficamente mediante un conjunto de curvas de indiferencia, que son líneas con pendiente negativa y que no se cortan entre sí. Las curvas están ordenadas, de manera que los puntos de una curva situada por encima son preferidos a los de cualquier curva situada por debajo. Toda combinación de bienes (punto del plano) pertenece a una curva de indiferencia (y sólo a una).*
Finalmente, la convexidad estricta y la monotonicidad juntas, lleva a curvas que son estrictamente convexas.*
Este conjunto de propiedades resulta en mapas de indiferencia como las que se muestran en la figura. Clica en ella para preguntarte algunas cuestiones sobre la interpretación de la figura.
Cada individuo tiene sus propias preferencias, posiblemente diferentes a las de los demás, aunque suponemos algunas características comunes en todas las preferencias de nuestros consumidores.
Estas propiedades* permiten representar gráficamente las preferencias de un consumidor a través de las curvas de indiferencia. Cada curva de indiferencia recoge los puntos (combinaciones de bienes) que son indiferentes para el consumidor. Además estas propiedades implican que por cada cesta pasa una curva de indiferencia y las curvas de indiferencia no pueden cruzarse. Así, todas las cestas están ordenadas (débilmente) según las preferencias del consumidor.
Estas propiedades* nos llevan a conjuntos de indiferencia finos (líneas) llamados curvas de indiferencia, con pendiente negativa y convexas.
Preferencias Curva de indiferencia Mapa de indiferencia Preferencias completas Preferencias transitivas Preferencias monótonas Preferencias convexas Preferencias continuas