(Concepto matemático)$\quad \quad$
Una combinación lineal convexa de dos cestas es una cesta compuesta por un porcentaje de las cantiades de bienes de una de las cestas y el resto (hasta el 100%) de la otra.
Gráficamente, todas las combinalciones lineales convexas entre dos puntos forman el segmento que une esos dos puntos.
Ejemplo
Dadas las cestas $(1,9)$ y $(9,1)$, el gráfico de la izquierda muestra la combinalción lineal convexa al 50%, el gráfico de la derecha muestra la combinación lineal convexa con el 75% de la cesta $(1,9)$ y el 25% de la cesta $(9,1)$:
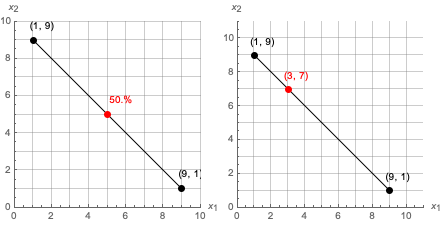- En el gráfico de la izquierda, el punto rojo $(5,5)$ se obtiene
$(0.5\cdot 1+0.5\cdot 9,0.5\cdot 9+0.5\cdot 1)=(5,5)$
cogiendo el 50% de cada una.
- En el gráfico de la derecha: El punto rojo, $(3,7)$, se obtiene $(0.75\cdot 1+0.25\cdot 9,0.75\cdot 9+0.25\cdot 1)=(3,7)$ cogiendo el 75% of (1,9) y el 25% de (9,1).
- En el gráfico de la derecha: El punto rojo, $(3,7)$, se obtiene $(0.75\cdot 1+0.25\cdot 9,0.75\cdot 9+0.25\cdot 1)=(3,7)$ cogiendo el 75% of (1,9) y el 25% de (9,1).