El problema de nuestro consumidor, como se dijo al inicio del capítulo, es decidir qué combinación de bienes consumir cuando dispone de una renta $m$ para gastar en dos bienes, $x_1$ y $x_2$, que el mercado le ofrece a precios $p_1$ y $p_2$.

Cuando conociste a Peter, John y Mary tuviste oportunidad de buscar su respuesta a esta pregunta de manera más o menos intuitiva. * Si no lo hiciste entonces, o quieres refrescar la memoria, puedes dedicarle ahora un momento. (Peter, John y Mary)

Desde entonces hemos dedicado un tiempo a trabajar sobre las posibilidades y sobre las preferencias. Lo que hemos aprendido, y las herramientas que hemos construido, van a servir para resolver de manera más formal y sistemática el problema de Peter, John y Mary... y muchos otros.

¿Qué combinación de bienes debería elegir un consumidor? La respuesta general, como en cualquier problema de elección, es; de entre las alternativas que puede, la mejor. Que adaptando al caso que estamos examinado, podemos reformular diciendo que la elección óptima para un consumidor es la cesta de su conjunto presupuestario para la que la función de utilidad tiene el valor más alto.

Comencemos con Peter. Le gusta consumir la mayor cantidad posible, le da lo mismo si son caramelos o nubes. Si cada caramelo cuesta 2 céntimos y cada nube sólo uno, ¿cuál será la cesta elegida?

Seguramente ya has llegado a la conclusión de que, si caramelos y nubes le parecen igual de buenos, lo mejor para Peter será gastarse el dinero en el que sea más barato, esto es, comprar sólo nubes. Aunque este es un caso muy sencillo, ¿cómo habríamos podido usar aquí nuestras herramientas?

Por un lado tenemos la recta de balance, que recoge todas las posibles combinaciones que podría comprar con 60 céntimos. La hemos expresado tanto gráfica como analíticamente:

Por otro lado hemos estudiado las preferencias de Peter y obtenemos su mapa de indiferencia, formado por curvas de indiferencia rectas con pendiente -1 (que refleja que siempre estaría dispuesto a intercambiar un caramelo por una nube, o viceversa, ya que le parecen igual de satisfactorios).

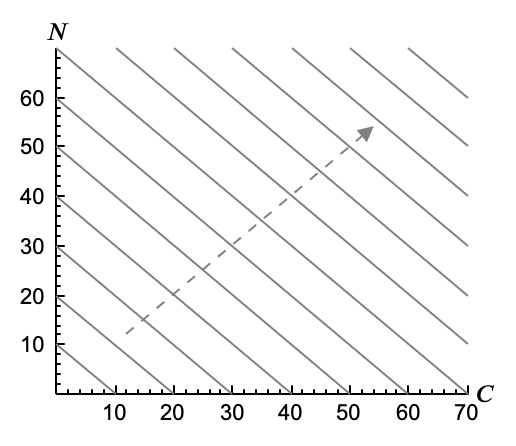
Si juntamos las dos figuras podremos identificar la solución. Cada punto de la recta de balance pertenece a una curva de indiferencia.* Recuerda que todo punto del plano pertenece a una (y solo a una) curva de indiferencia. Vemos dibujadas algunas de las curvas de Peter, como ejemplo, pero sabemos que las demás están ahí aunque no estén dibujadas (podríamos pensar que son transparentes). Y un punto es preferido a otro si pertenece a una curva más alta. Mirando la figura, de todos los puntos de la recta de balance, el que pertenece a una curva más alta es el (0, 60), como habíamos previsto (hemos dicho que se iba a gastar el dinero en nubes, y como cada nube cuesta un céntimo, con 60 céntimos puede comprar 60 nubes).* Más formalmente, como la recta de balance es $2C+N=60$, si no va a comprar caramelos, $C=0$, se cumplirá que $N=60$.

Por supuesto, existen curvas más altas (esto es puntos mejores que el (0, 60), pero quedan fuera de su alcance porque cuestan más de 60 céntimos.

El caso de Peter es muy sencillo, pero nos ha servido para ver cómo, usando la recta de balance y el mapa de indiferencia, podemos visualizar la solución al problema.

Ejemplo

Pasemos ahora a pensar en Mary. Su conjunto presupuestario es idéntico al de Peter. Pero ella sólo obtiene satisfacción cuando come un caramelo con cada nube, por lo que un exceso de cualquiera de los dos le resulta inútil.

Dibujando en una misma figura tanto la recta de balance como el mapa de indiferencia de Mary tenemos:

De nuevo, si se trata de elegir el mejor punto de la recta de balance la respuesta está clara en términos gráficos (¿no?* Haz click en "Ver Sol". ), unque hay que ver cómo calcular las coordenadas del punto identificado como solución.

Para hacer el cálculo podemos seguir dos caminos distintos:

• Si optamos por un razonamiento genérico podemos pensar que Mary en realidad consume pares formados por un caramelo y una nube. Así, cada par costaría $p_C+p_N=3$. Con 60 céntimos podría comprar $\frac{60}{3}=20$ pares, esto es, 20 caramelos y 20 nubes.
• Podemos usar nuestras herramientas. Vemos que el punto elegido es el vértice de una de las curvas de indiferencia, y los vértices son los puntos en que $C=N$ (no sobran caramelos ni nubes). Además es un punto de la recta de balance, por lo que tendrá que cumplir la ecuación $2C+N=60$. El punto elegido será la solución al sistema formado por las dos ecuaciones \[ \left. \begin{array}{c}C=N \\ 2C+N=60 \end{array} \right\} \quad \Longrightarrow \quad \begin{array}{c}C=20 \\ N=20 \end{array} \]

Observa que en este caso la figura nos ha mostrado la solución, pero para calcularla hemos usado la ecuación de la recta de balance y la ecuación que cumplen los vértices de las curvas de indiferencia.

Ejemplo

Veamos en tercer lugar el caso de John. Sus alternativas (conjunto presupuestario) son las mismas que las de sus primos, pero sus preferencias son diferentes. Recuerda que para comparar cestas lo que John hace es multiplicar el número de caramelos por el de nubes. Esto da lugar a un mapa de indiferencia con curvas estrictamente convexas (preferencias de John). La idea de multiplicar las coordenadas puede resultar algo artificiosa, pero las curvas convexas recogen una propiedad que nos parece atractiva (por realista), que es el decrecimiento de la RMS. A medida que un consumidor aumenta su consumo de un bien reduciendo el del otro, cada vez está menos dispuesto a renunciar al bien que disminuye para conseguir nuevas unidades del bien que se va haciendo más abundante.

Para las preferencias de John elegir la cesta óptima resulta más complejo que con sus primos. Por eso, antes de intentar resolverlo haremos una discusión más general del caso en que las curvas de indiferencia son estrictamente convexas (como pasa con las de John, que son del tipo Cobb-Douglas, pero también con muchas otras).

Con este tipo de curvas, el cálculo proporciona un enfoque más mecánico (y potente). Pero de todos modos, empezaremos proponiendo (y resolviendo) el problema gráficamente.

Solución gráfica

Consideremos un consumidor con preferencias monótonas y estrictamente convexas, con una renta de $m$ para gastar en los bienes 1 y 2. Los precios de mercado son $p_1$ y $p_2$.

En la misma figura dibujamos la recta presupuestaria y las curvas de indiferencia del consumidor. ¿Qué cesta seleccionará? Antes de continuar, intenta obtener un resultado haciendo clic en la figura y respondiendo a las preguntas.

¿Qué nos ha enseñado lo visto en la figura?

En primer lugar, la figura muestra que el óptimo debe ser un punto de la recta presupuestaria; el consumidor no puede permitirse nada por encima de la recta, y en los puntos por debajo de ella le sobra dinero (que podría gastar para obtener más de ambos bienes y, por monotonicidad, más utilidad).

Además, si la curva de indiferencia corta con la recta presupuestaria en un punto determinado, la parte de la recta presupuestaria que está por encima de la curva está formada por cestas asequibles y preferidas. Por tanto, ese punto no es el buscado (es posible obtener uno mejor).

Esto significa que la cesta óptima debe ser un punto en la recta presupuestaria donde la curva de indiferencia no corta a la recta.

Condición de tangencia

Cuando dos curvas (o una curva y una recta) se encuentran en un punto sin cortarse, se dice que son tangentes. La tangencia implica que en ese punto ambas curvas tienen la misma pendiente.

Se sabe que la pendiente de la recta presupuestaria viene dada por la relación de precios, $-\frac{p_1}{p_2}$, y la pendiente de una curva de indiferencia en cualquier punto es la relación marginal de sustitución, RMS. Así, se puede afirmar que en el punto óptimo, $(x_1^*, x_2^*)$, se cumple la siguiente ecuación,

Esto se conoce como la condición de tangencia Al mirar la ecuación es importante darse cuenta de que no decimos que la RMS es el cociente de precios. La RMS es la pendiente de la curva, y $-\frac{p_1}{p_2}$ es la pendiente de la recta presupuestaria. Son dos cosas distintas, con significados diferentes.
En el punto óptimo sus valores coinciden, en otros puntos no. .

Como punto de la recta presupuestaria, el punto seleccionado también debe satisfacer la ecuación presupuestaria: \[ p_1 x_1^* + p_2 x_2^* = m \]

Dados unos precios y una renta concretos, el sistema formado por la condición de tangencia y la ecuación presupuestaria permite determinar la cesta óptima (o cesta demandada por el consumidor).

Significado económico

En términos económicos el cumplimiento de la ecuación de la recta presupuestaria significa que el consumidor elegirá una cesta de bienes en la que se gastará toda su renta. Pero, ¿cómo se puede interpretar la condición de tangencia?

La RMS da la valoración subjetiva del bien 1 por parte del consumidor expresada en unidades del bien 2, es decir, cuánto bien 2 está dispuesto a dar (o aceptar) a cambio de una unidad del bien 1. La relación de precios indica la valoración del mercado, es decir, cuánto bien 2 exige (u ofrece) el mercado a cambio de una unidad del bien 1.

Considera un punto en la recta presupuestaria donde $|\mathrm{RMS}| > \frac{p_1}{p_2}$. Por una unidad del bien 1, el mercado pide menos bien 2 del que el consumidor está dispuesto a pagar. Por tanto, comprar el bien 1 aumenta la satisfacción del consumidor. Si la desigualdad es en sentido contrario, el consumidor podría mejorar vendiendo el bien 1, dado que el mercado paga por él más que el valor que le otorga. En resumen, sólo cuando hay igualdad (tangencia) el consumidor no puede mejorar su posición mediante el intercambio, ya que ni la compra ni la venta producen un resultado ventajoso.

Otra forma de verlo

Teniendo en cuenta que la RMS puede calcularse como la relación (negativa) de las utilidades marginales, la condición de tangencia puede reescribirse como \[ -\frac{\mathrm{UMg}_1(x_1^*, x_2^*) }{\mathrm{UMg}_2(x_1^*, x_2^*) } = -\frac{p_1}{p_2} \quad \Longrightarrow \] \[ \Longrightarrow \quad \frac{\mathrm{UMg}_1(x_1^*, x_2^*) }{p_1 } = \frac{\mathrm{UMg}_2(x_1^*, x_2^*)}{p_2} \quad \]

Si la utilidad marginal de un bien es el aumento de la utilidad debido a un aumento del consumo del bien en una unidad, y el precio es lo que hay que pagar por esa unidad, el cociente puede interpretarse como aumento de la utilidad por cada euro adicional gastado en el bien. Por eso ese cociente se denomina utilidad marginal del dinero gastado en el bien.

Redactada de este modo, la condición de tangencia indica que, en el óptimo, las utilidades marginales del dinero gastado en ambos bienes son las mismas. Si no es así, el cambio de un euro del bien con menor utilidad marginal del dinero al otro, daría lugar a un aumento de la utilidad total (la reducción debida a tomar un euro de un bien es menor que el aumento de utilizar ese euro en el otro bien).

Volvamos ahora al caso de Juan. Ya hemos recordado que sus curvas de indiferencia son estrictamente convexas y hemos visto su función de utilidad, $\mathrm{U}(C, N) = C\cdot N$, con una tasa marginal de sustitución de $\mathrm{RMS}(C, N) =- \frac{N}{C}$.

Ahora podemos utilizar lo que acabamos de aprender para calcular la solución del problema de Juan. La figura muestra su presupuesto completo y el mapa de indiferencia (las preferencias de John).

La cesta que maximiza la utilidad de John, dada su renta y los precios actuales, será el punto de la recta presupuestaria donde una de las curvas de indiferencia es tangente.

Para calcularlo, resolvemos el sistema de ecuaciones formado por la ecuación presupuestaria y la condición de tangencia \[ \left. \begin{array}{c} 2C+N=60 \\ -\frac{N}{C} = -\frac{2}{1} \end{array}\right\} \begin{array}{ccl} &2C+2C=60 & C=\frac{60}{4}= 15 \\ N=2C & & N=30 \end{array} \]

La mejor cesta que puede elegir John es $(C, N) = (15, 30)$. Si no lo encontraste en su momento, puedes comprobar ahora que esta combinación consigue la mayor sonrisa de John en Peter, John y Mary.

Ejemplo

¿Funciona siempre la condición de tangencia?

Las preferencias de Peter y de Mary son dos casos en los que la solución NO es un punto de tangencia.* Recuerda que la tangencia significa matemáticamente igualdad de pendientes. En el caso de Mary la solución está en un vértice, donde la pendiente no está definida (la RMS no tiene sentido). En el caso de Peter, la RMS es constante y puede ser distinta al cociente de precios en cuyo caso también en el óptimo las pendientes serán distintas. En la siguiente página veremos con más detalle estos casos, y algunos más, en los que la condición de tangencia no funciona, lo que nos obligará a pensar un poco más.

Sin embargo, podemos hacer una afirmación relacionada que sí tiene carácter general: Un punto en el que se cortan la recta presupuestaria y la curva de indiferencia nunca puede ser el óptimo. Inevitablemente, a un lado del punto de corte, la recta presupuestaria estará por encima, y al otro lado, estará por debajo. Pero esto significa que hay puntos alcanzables (ya que están en la línea) preferidos al punto de corte (que entonces no puede ser un óptimo).

Resumiendo:

• Utilizando los conceptos desarrollados en este capítulo, el problema del consumidor sobre cómo gastar mejor su renta puede expresarse tanto gráfica como matemáticamente:
  • Gráficamente: ¿qué punto de la recta presupuestaria pertenece a una curva de indiferencia más alta?
  • Matemáticamente: ¿qué combinación de bienes $(x_1, x_2)$ de las que satisfacen la ecuación presupuestaria maximiza el valor de la función de utilidad?
• Un punto de corte entre la recta de balance y la curva de indiferencia no puede ser un punto óptimo.
• Si las preferencias son monótonas y estrictamente convexas:
  • La cesta óptima será el punto en el que una curva de indiferencia sea tangente a la recta de balance.* Pueden darse excepciones cuando las curvas de indiferencia cortan los ejes, como se verá en la página siguiente, en el caso de las preferencias cuasilineales.
  • La condición de tangencia dice que en la cesta óptima la valoración subjetiva del consumidor para el bien 1 en unidades del bien 2 (RMS) será igual a la valoración del mercado (el cociente de precios dice cuánto pide o paga el mercado por una unidad del bien 1).
  • Analíticamente se puede calcular la cesta demandada por el consumidor resolviendo el sistema de ecuaciones formado por la ecuación presupuestaria y la condición de tangencia: \[ \left. \begin{array}{c} p_1 x_1 + p_2 x_2 = m \\ \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \end{array} \right\} \]

Problema de decisión   Elección óptima   El problema del consumidor   Cesta demandada   Condición de tangencia   Utilidad marginal del dinero gastado en un bien