Supongamos una cesta con ciertas cantidades de bienes, $(x_1^o, x_2^o)$, que pertenece a la recta presupuestaria de un consumidor.

Sabemos que los precios de mercado son $p_1=4$ y $p_2=8$. También sabemos que en ese momento el valor de la tasa de sustitución es $\mathrm{RMS}(x_1^o, x_2^o) = -1$.

¿Podría ser el punto $(x_1^o, x_2^o)$ el elegido por el consumidor (su demanda)?

"Esa pregunta no puede responderse por falta de información. No conocemos el punto exacto ni la función de utilidad, por lo que no podemos calcular nada". ¿VERDADERO O FALSO? ¿Cómo justificarías tu respuesta? Sol.

• Sabemos que $\mathrm{RMS}(x_1^o, x_2^o) = -1$. Esto significa que intercambiar una unidad del bien 1 por una unidad del bien 2, mantiene al consumidor indiferente.
• Dados los precios, es posible calcular el cociente $-\frac{p_1}{p_2} = -\frac{4}{8} = 0,5$. Anteriormente, hemos interpretado el cociente de precios como lo que vale una unidad del bien 1 en el mercado en unidades del bien 2 (precio relativo). En este caso, una unidad del bien 1 puede comprarse (o venderse) a cambio de la mitad de una unidad del bien 2.

¿Qué pasaría con la utilidad del consumidor si vende el bien 1 a cambio del bien 2? Para mantener su utilidad constante la RMS dice que si entrega una unidad de $x_1$ necesitaría una unidad de $x_2$. Pero el mercado sólo le pagaría la mitad. Por tanto, vender el bien 1 para comprar el bien 2 le perjudicaría, ya que el mercado no le paga con suficiente bien 2 para sustituir el bien 1 vendido. Pero también existe la posibilidad contraria. Estaría dispuesto a pagar una unidad del bien 2 a cambio de una unidad del bien 1, pero el mercado sólo le pide la mitad. Por lo tanto, comprar el bien 1 es un intercambio ventajoso; terminaría en un punto mejor que el inicial, porque habría pagado menos el bien 2 que lo que le habría dejado indiferente.

¿Puedes replicar el razonamiento si nos fijamos en otro punto, $(x_1^1, x_2^1)$, del que sabemos que $\mathrm{RMS}(x_1^1, x_2^1) = -0.25$? (los precios siguen siendo $p_1=4$ y $p_2=8$).Sol.

En general, el razonamiento es sencillo. Si el mercado valora el bien 1 más que yo, vender el bien 1 es un buen negocio porque me pagan más de lo que creo que vale. Si la valoración del mercado es inferior a la mía, salgo ganando al comprar el bien 1, ya que tengo que pagar menos de lo que estaría dispuesto a pagar. Si mi valoración (RMS) coincide con la del mercado (cociente de precios), no hay oportunidad de negocio, por lo que estoy en un punto óptimo.* A algunas personas les parece contradictorio que en el punto óptimo no haya ninguna oportunidad de negocio. Pero en realidad, es el óptimo precisamente porque ya se han aprovechado todas las oportunidades de negocio posibles. Al igual que desde la cima de una montaña cualquier camino es hacia abajo, desde el punto óptimo cualquier cambio sólo puede ser a peor (ya que estoy en el mejor de los posibles).

Este razonamiento se resume en la condición de tangencia, al decir que en el punto óptimo debe cumplirse: \[\mathrm{RMS}(x_1^*, x_2^*) = -\frac{p_1}{p_2} \]

¿Qué significa gráficamente que en un punto de la recta el valor de la RMS difiera del cociente de precios? Sol.

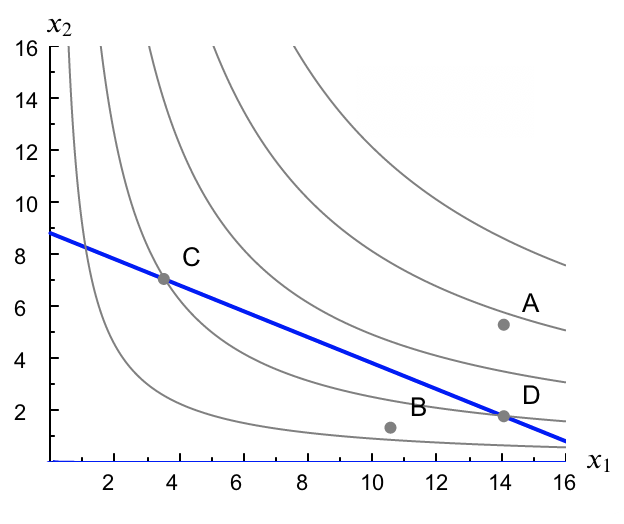
¿Podría ser alguno de los puntos marcados en la figura el punto $(x_1^o, x_2^o)$ Sabemos que $(x_1^o, x_2^o)$ está en la recta presupuestaria, $\mathrm{RMS}(x_1^o, x_2^o) = -1$ y además $\frac{p_1}{p_2}=0.5$. ? ¿Y el $(x_1^1, x_2^1)$ Sabemos que $(x_1^1, x_2^1)$ también está en la recta presupuestaria, $\mathrm{RMS}(x_1^1, x_2^1) = -0.25$ y $\frac{p_1}{p_2}=0.5$. ? Sol.

La figura permite ver fácilmente la dirección del movimiento a lo largo de la línea recta que mejoraría el consumidor.

Ahora iremos un paso más allá: Qué ocurrirá cuando se mueva según el razonamiento anterior. Observa la siguiente figura. Puedes ver un punto de partida $(x_1^o, x_2^o)$ y a la derecha tienes los valores de $\mathrm{RMS}(x_1^o, x_2^o)$ y el cociente de precios, $-\frac{p_1}{p_2}$. Hay que decidir si se aumenta o se reduce la cantidad de $x_1$ (se entiende que los cambios de $x_1$ se hacen cambiando por $x_2$ a precios de mercado, por lo que al cambiar uno también cambia el otro). Los botones '-' y '+' le permitirán ejecutar la variación.

• ¿Dónde hay que centrarse para tomar la decisión de comprar o vender un bien 1?Sol.
  Si ha respondido que "en la figura", la respuesta no es incorrecta, pero en este punto, tenemos que hacer hincapié en que debe centrarse en la comparación entre la RMS y el cociente de precios.
• ¿Cuándo hay que pulsar el botón "+"? Sol.
  Si $|\mathrm{RMS}| > \frac{p_1}{p_2}$, porque significa que el mercado ofrece el bien 1 a un precio relativo inferior a la valoración del consumidor.
• ¿Qué sucede con el valor de $\frac{p_1}{p_2}$ cuando se cambia $x_1$? Sol.
  Nada de nada. Los precios son datos que no dependen de la cantidad consumida.
• ¿Y qué pasa con el valor de la RMS? Sol.
  Al aumentar $x_1$ (con la correspondiente reducción de $x_2$), el valor de la RMS disminuye. Si reducimos $x_1$, la RMS aumenta.
• Observa la diferencia entre el cociente de precios y la RMS. ¿Mover $x_1$ aumenta o disminuye esa diferencia? Sol.
  Si se pulsa el botón correcto (para mejorar en utilidad), la diferencia entre la RMS y el cociente de precios debería disminuir (en valor absoluto).
• Sigue pulsando el "+" o el "-" (según sea necesario). ¿Terminará alguna vez el proceso?Sol.
  La diferencia debería bajar a 0.
  Si es así, ¿qué pasará con la figura? Sol.
  Cuando los valores de la RMS y del cociente de precios son iguales, la curva de indiferencia de $(x_1^o, x_2^o)$ será tangente a la recta presupuestaria. Es la elección óptima.
• El botón 'Nuevo ejemplo' genera una nueva situación inicial. Puedes repetir el proceso para ver cómo en algunos casos utilizarías el botón '+' y en otros el botón '-'. Ahora es un buen momento para ver que, mirando la figura identificamos el botón correcto más rápido que comparando los valores. Pero no olvides que la figura es la herramienta, y lo importante es entender la lógica de la comparación entre la RMS y el cociente de precios.