|
La demanda del consumidor 2.- Variaciones de renta |
Sea una situación inicial en la que un consumidor está consumiendo su cesta óptima, dada su renta y los precios vigentes en los mercados para los bienes 1 y 2. (Es un consumidor con preferencias bien comportadas Monótonas y estrictamente convexas. ).
¿Qué crees que haría el consumidor si su renta aumentara?
Usaremos las herramientas que tenemos para estudiar las posibilidades, e incluso introduciremos nuevos conceptos. Pero antes dedica unos minutos a considerar las siguientes posibles respuestas a la pregunta. ¿Quizá alguna de ellas es la que tú darías? Cuidado, sólo una de ellas es correcta.
¡Correcto!
Dado que los precios no han cambiado, consumir lo mismo, o menos, de los dos bienes costaría menos dinero. Y con preferencias monótonas no tendría sentido dejar dinero sin gastar. Pero sí podría haber una cesta más cara que tuviese más de un bien y menos del otro que la inicial.Incorrecta.
¿Qué significa 'una cantidad total de bienes'? Quizá el bien 1 son manzanas y el bien 2 clases de tenis. ¿Tiene sentido decir que en la cesta (8, 2), que son 8 manzanas y dos clases de tenis, ha consumido 10 en total? ¿10 qué?De las anteriores afirmaciones (y sus explicaciones) podemos sacar al menos un par de cosas:
Primero, debemos ser cuidadosos con el lenguaje. En este caso al hablar de una cesta de bienes (vector), algunas afirmaciones no tienen sentido. No hay una 'cantidad de bienes', sino una 'cantidad de cada bien'. Es cierto que estamos acostumbrados a hablar en dinero, y así entendemos que un consumo de 100 euros es mayor que uno de 80. Pero eso no nos dice lo que ha pasado con el consumo de cada bien.
La precisión en el lenguaje, evitando sobrentendidos y ambigüedades, es muy importante tanto al transmitir información como al construir el propio razonamiento. De hecho, la exigencia de precisión es una de las principales aportaciones que el uso de expresiones y razonamientos matemáticos aporta a la microeconomía.
En segundo lugar, podemos ver que la única afirmación correcta no proporciona una respuesta muy concreta. Pero eso puede pasar con muchas preguntas, y eso sólo significa que hay diferentes posibilidades, en este caso dependiendo de las preferencias de los consumidores.* En todo caso, aunque no podamos concretar lo que sí va a pasar cuando aumente la renta, sí podemos decir que ciertas respuesta, como que consuma menos de ambos bienes, no podrían darse.
Veamos la siguiente figura. En ella tenemos dos consumidores diferentes que deben tomar su decisión ante el mismo conjunto presupuestario. Cada uno de ellos demanda inicialmente una cesta diferente, pero lo que nos interesa ahora es su respuesta a una variación en su renta. El control $\Delta m$ te permite proponer una variación (positiva o negativa). Hazlo, y observa las respuestas.
Mira la figura de la izquierda* No es que sea relevante saberlo en este momento, pero son las preferencias de Amanda. ¿Qué ocurre si aumentas la renta ($\Delta m > 0$)?
Como hemos visto ya anteriormente, un aumento de la renta desplaza la recta de balance hacia la derecha, en paralelo La pendiente de la recta de balance la da el cociente de precios, $-\frac{p_1}{p_2}$, que no ha cambiado. .
Vemos que aumenta la cantidad consumida de los dos bienes. ¿Te parece una respuesta razonable? Sol.
Ahora observa la figura de la derecha. ¿Cómo responde este consumidor al aumento de la renta? Vemos que aumenta su consumo de bien 2, pero reduce su consumo del bien 1. ¿Es un comportamiento muy raro? Sol.
Aunque ante el mismo aumento de renta uno y otro consumidor responden de forma diferente (opuesta, en lo que se refiere al bien 1), ambas respuestas son perfectamente razonables. Simplemente los dos consumidores tienen preferencias diferentes.
Decimos que un bien es Normal para un consumidor si este demanda mayor cantidad del bien cuando aumenta su renta (o menor cuando $m$ disminuye). Si la respuesta del consumidor es reducir su consumo de un bien cuando su renta aumenta decimos que ese bien es Inferior para ese consumidor.
Dos observaciones:
¿Cómo saber si un bien es Normal o Inferior para un consumidor?
Puesto que hablamos de preferencias, la respuesta más obvia es: preguntando al consumidor. O bien, como hemos hecho arriba, mirando las figuras que representan las preferencias.
En nuestro escenario, con las preferencias captadas por las funciones de utilidad, podríamos calcular las cestas óptimas antes y después de la variación de ingresos, para tener una respuesta más precisa.
EjemploPero hay una forma más potente de responder a la pregunta, usando las funciones de demanda individual. Suponiendo que las tengamos, o sepamos calcularlas, podemos preguntarnos cómo varía el valor de las cantidades demandadas ante un aumento de la renta. Esto nos permitirá responder a la pregunta de si un bien es Normal o Inferior. Por ejemplo, en el caso de John ya hemos calculado anteriormente que sus funciones de demanda son
\[ C(p_C, p_N, m) = \frac{m}{2\cdot p_C} \quad \quad N(p_C, p_N, m) = \frac{m}{2\cdot p_N} \]Viendo estas funciones está claro que a mayor valor de $m$ mayor demanda tanto de $C$ como de $N$. Ambos bienes son Normales.
De hecho, podríamos expresar las definiciones de bien Normal e Inferior usando las derivadas parciales de las funciones de demanda respecto de $m$:
Un bien, $x_i$, es Normal para un consumidor siempre que, dada la función de demanda individual $x_i = x_i(p_1, p_2, m)$, la derivada parcial respecto de $m$ sea positiva,
\[ \frac{\partial x_i(p_1, p_2, m)}{\partial m} > 0 \]Igualmente, el bien será Inferior si:
\[ \frac{\partial x_i(p_1, p_2, m)}{\partial m} < 0 \]Ejemplo
¿Y para Mary? ¿Son los caramelos y las nubes bienes Normales o Inferiores? Sol.
Hemos calculado que las funciones de demanda eran
\[ C(p_C, p_N, m) = \frac{m}{ p_C + p_N} \] \[ N(p_C, p_N, m) = \frac{m}{p_C + p_N} \]En ambas funciones vemos que mayor valor de $m$ implica mayor cantidad demandada. Por tanto ambos bienes también son Normales para Mary.
Vamos a construir dos herramientas que representan gráficamente la relación entre la renta y la decisión del consumidor.
La primera es la llamada senda de expansión de la renta.
Ya hemos visto gráficamente la respuesta a una variación de renta, que lleva de una situación inicial a una nueva. Pero podemos, sin cambiar los precios, añadir a la figura nuevos valores de $m$, con sus correspondientes cestas óptimas.
En la siguiente figura se ve inicialmente la cesta demandada para unos precios y una renta, pero puedes activar distintos valores de $m$ con sus correspondientes puntos óptimos.
Aunque no entramos en una demostración formal, podemos intuir que si pusiéramos muchos valores de $m$ cercanos entre sí los puntos óptimos irían formando una línea (activa 'Senda de expansión de la renta').
Dados unos precios fijos, llamamos senda de expansión de la renta (o también línea renta-consumo) a la línea formada por los puntos que serían óptimos para algún valor de $m$.
Las siguientes cuestiones intentan ayudarte a comprender la información ofrecida por la senda de expansión.
Observa una vez más la figura. ¿Qué tienen en común todos los puntos que forman la senda de expansión? Cada uno es el punto óptimo de una recta de balance, para cierto valor de $m$. Cada uno de esos puntos se calcularía planteando el sistema con la ecuación presupuestaria y la condición de tangencia. Pero mientras la ecuación presupuestaria es diferente para cada valor de $m$, la renta no está en la condición de tangencia. Resumiendo, dados unos precios fijos todos los puntos de la senda de expansión cumplen la misma ecuación de tangencia,
\[ \mathrm{RMS}(x_1, x_2) = - \frac{p_1}{p_2} \]Por ejemplo, en el caso de John, con $\mathrm{U}(C, N) = C\cdot N$, ¿cuál sería la senda de expansión si $p_C=2$ y $p_N=4$? Sol.
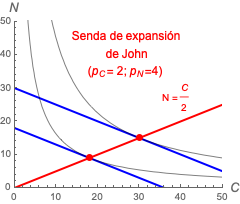
¿Cómo cambiaría si los precios hubieran sido $p_C=3$ y $p_N=2$? Sol.
¿Y qué pasa con aquellas preferencias en las que la condición de tangencia no funciona, como el de Mary? Ya hemos visto que puede haber más de un motivo, y en cada caso habría que buscar la estrategia adecuada.
Ejemplo
Las preferencias de Mary vienen dadas por la función de utilidad $\mathrm{U}(C, N) = \mathrm{Min}\{ C, N \}$.
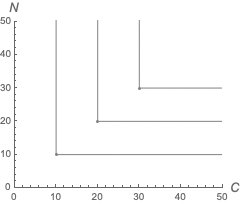
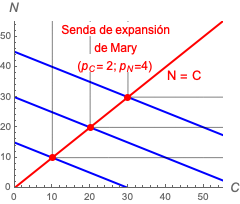
Igual que con John, podemos preguntarnos cómo cambiará la senda de expansión si cambiamos los precios a $p_C=3$ y $p_N=2$? Sol.
La senda de Mary no cambia al variar los precios, ya que los puntos óptimos siguen siendo los vértices (que vienen dados por las preferencias, no por los precios).
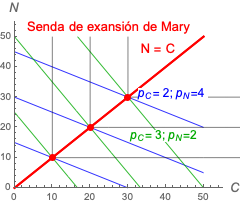
Los ejemplos de John y Mary nos han dado sendas de expansión rectas. Pero en la figura de más arriba la senda de expansión era una curva. En realidad las sendas de expansión pueden tener diferentes formas, dependiendo de las preferencias. Normalmente buscamos mantener las operaciones lo más sencillas posible y nuestras funciones de utilidad suelen dar lugar a sendas de expansión rectas, pero puede haber muchos otros casos.
Example
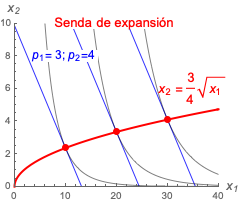
La senda de expansión de la figura representada arriba corresponde a la función de utilidad $\mathrm{U}(x_1, x_2) = 2 \sqrt{x_1} + \log{x_2}$.
¿Cómo calcular la senda de expansión para los precios $p_1=3$ y $p_2=4$ ?
Necesitamos la RMS para poder construir la condición de tangencia.
Las utilidades marginales son \[ \mathrm{UMg}_1(x_1, x_2) = \frac{2}{2 \sqrt{x_1}} = \frac{1}{\sqrt{x_1}} \quad \quad \mathrm{UMg}_2(x_1, x_2) = \frac{1}{x_2} \]
TEl cocente de las utilidades marginales nos da la relación marginal de sustitución:
Igualando la RMS al cociente de los precios tenemos la condición de tangencia
\[ - \frac{x_2}{\sqrt{x_1}} = - \frac{3}{4} \]de donde despejamos $x_2$ para tener la ecuación de la senda de expansión \[ x_2 = \frac{3}{4} \sqrt{x_1} \]
La segunda forma de representar gráficamente la relación entre renta y consumo de bienes son las llamadas curvas de Engel. Más concretamente, dados unos valores fijos de los precios llamamos curva de Engel de un bien Habrá una curva para el bien 1 y otra para el bien 2. a la curva que relaciona el nivel de renta con la cantidad demandada de ese bien.
Esta figura corresponde al bien 2 para el consumidor del último ejemplo, dados unos precios $p_1=3$ y $p_2=4$. ¿Sabrías calcularla, sabiendo que su función de demanda del bien 2 es $x_2(p_1, p_2, m) = \frac{p_1 \left( \sqrt{\frac{p_1+4m}{p_1} } -1 \right)}{2 p_2}$? Sol.
La curva de Engel de la figura tiene pendiente positiva. ¿Tienes alguna interpretación? Sol.
Cuando un bien sea Inferior su curva de Engel tendrá pendiente negativa. Como se ha visto en el caso de la senda de expansión, dado que con $m=0$ no es posible demandar nada, un bien puede ser Inferior a partir de cierto nivel de renta, siempre que por debajo de ese nivel fuera Normal.
¿Qué pasaría si cambiáramos los precios? Sol.
Example
¿Puedes calcular la curva de Engel de Amanda para el bien 2 cuando los precios son $p_1=3$ y $p_2=2$ ? (La RMS de Amanda era $\mathrm{RMS}(x_1, x_2) = -\frac{x_2^{1/2}}{x_1^{1/2}} = -\sqrt{\frac{x_2}{x_1}}$)
Anteriormente habíamos calculado las funciones de demanda individual de Amanda, por lo que bastaría con coger la del bien 2 y sustituir los precios.
Si no tuviéramos esas funciones calculadas podríamos plantear el problema utilizando directamente los precios. Así, el sistema a resolver (condición de tangencia y ecuación presupuestaria) sería: \[ \left. \begin{array}{c} -\sqrt{\frac{x_2}{x_1} }= -\frac{3}{2} \\ 3 \cdot x_1+ 2 \cdot x_2= m \end{array} \right\} \quad \Longrightarrow \quad \begin{array}{c} x_1 = \frac{2\cdot m}{15} \\ x_2 = \frac{3\cdot m}{10} \end{array} \]
La curva de Engel obtenida para el bien 2 es una recta que sale del origen con pendiente $\frac{3}{10}$. El bien 2 es normal para cualquier nivel de renta, puesto que toda la curva tiene pendiente positiva.
Si, como decíamos al principio, recuperamos la función de demanda de bien 2 de Amanda que se calculó antes,\[ x_2(p_1, p_2, m) = \frac{p_1 \cdot m}{p_2 \cdot (p_1 + p_2)} \]
basta con sustituir los precios para comprobar que el resultado es el mismo: \[ x_2(3, 2, m) = \frac{3 m}{2 (3 + 2)} = \frac{3 m}{10} \]
Dados unos precios fijos, ¿cómo responde un consumidor a un cambio en su renta?
Bien Normal
Bien Inferior
Senda de expansión de la renta
Curva de Engel