Supongamos las preferencias de John, $\mathrm{U}(C, N) = C\cdot N$, y que éste dispone de una renta $m=60$ céntimos para gastar en caramelos y nubes a precios $p_C=3$ y $p_N = 2$. ¿Cómo respondería John a un aumento de 30 céntimos en su renta?

Ya habíamos calculado la relación marginal de sustitución de John, que era $\mathrm{RMS}(C, N) = -\frac{N}{C}$. En la situación inicial planteamos la ecuación presupuestaria y la condición de tangencia

\[ \left. \begin{array}{c} 3 \cdot C+ 2 \cdot N=60 \\ -\frac{N}{C} = -\frac{3}{2} \end{array} \right\} \]

Despejando $N$ en la segunda ecuación y sustituyendo en la primera obtenemos\[ C^* = 10 \quad \quad N^* = 15 \]

Con el aumento de renta el nuevo valor es $m'=60+30=90$. Repetimos el cálculo para este caso:

\[ \left. \begin{array}{c} 3 \cdot C+ 2 \cdot N=90 \\ -\frac{N}{C} = -\frac{3}{2} \end{array} \right\} \quad \Longrightarrow \quad \begin{array}{c} C'=15 \\ N' = 22.5 \end{array} \]

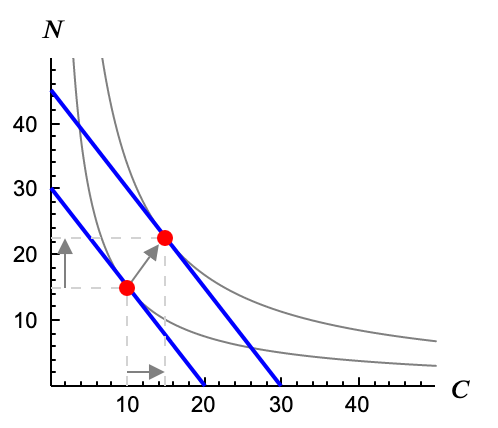
Al aumentar la renta John aumenta su consumo de los dos bienes. Tanto caramelos como nubes son para John bienes Normales.