Ya sabemos resolver el problema de un consumidor para una renta y unos precios concretos. Pero, ¿qué pasa si renta o precios cambian?

Calcular la cesta demandada por un consumidor para distintos valores de renta y precios resolviendo una y otra vez el mismo problema con distintos datos puede ser muy pesado y poco operativo.

Otra posibilidad es intentar resolver el problema de manera genérica, sin usar unos datos concretos. La idea es no tener que repetir las mismas operaciones para cada renta o precios. El resultado tendrá además importantes ventajas, como iremos viendo.

Ejemplo 

Como has podido ver en el ejemplo Si no lo has trabajado deberías hacerlo antes de seguir adelante. , la solución al problema cuando no conocemos los valores de los datos no es una cesta concreta, sino un par de funciones (una para cada bien). Cada una de ellas nos dice la cantidad del bien que resolvería el problema dependiendo de los valores que tomen los datos.

En el ejemplo hemos obtenido

\[ C = \frac{m}{p_C + p_N} \quad \quad N = \frac{m}{p_C + p_N} \]

En general llamamos función de demanda individual de un bien $i$ a la función que nos da la cantidad $x_i$ de ese bien que el consumidor demandaría, dependiendo de los precios y la renta.* Ten en cuenta que lo que resuelve el problema es una combinación de bienes $(x_1^*, x_2^*)$, por lo que el resultado del problema es una función para cada bien.

Así, buscamos un par de funciones

\[ x_1^* = x_1(p_1, p_2, m) \quad \quad x_2^* = x_2(p_1, p_2, m) \]

La manera de buscar esas funciones depende del tipo de preferencias (como ya hemos visto en distintos ejemplos cuando teníamos datos concretos). En el caso que consideramos más habitual, de preferencias bien comportadas Llamamos preferencias bien comportadas a aquellas que cumplen todas las propiedades propuestas. No sólo son completas y transitivas, sino que también son contínuas, monótonas y estrictamente convexas. , obteníamos la condición de tangencia.

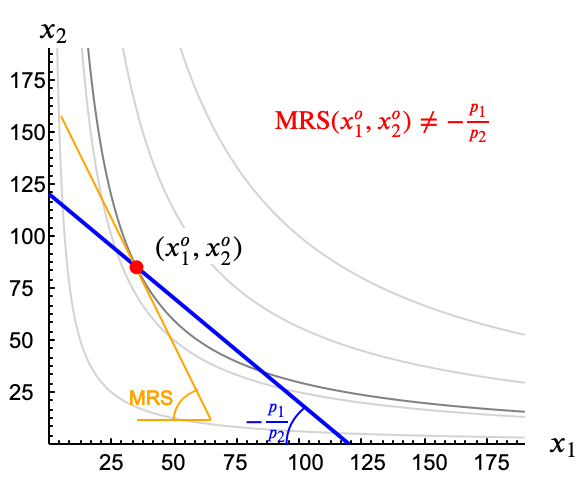
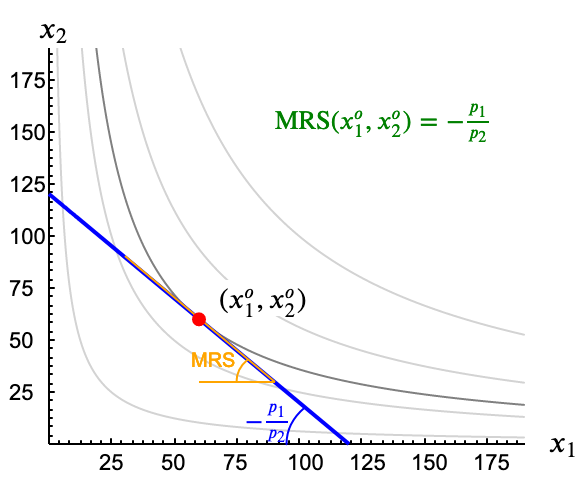
La curva de indiferencia más alta que puede alcanzar un consumidor es aquella que toca, sin cortarla, a su recta de balance. Si dos curvas (o una curva y una recta) son tangentes en un punto su pendiente en ese punto es la misma De hecho se define pendiente de una curva en un punto como la pendiente de la recta tangente a la curva en ese punto. .

Si conocemos, o sabemos calcular, la $\mathrm{RMS}(x_1, x_2)$ del consumidor podemos construir la ecuación correspondiente a la expresión anterior. Sabemos que la pendiente de la recta de balance viene dada por el cociente de los precios, $-\frac{p_1}{p_2}$, mientras que la relación marginal de sustitución es la pendiente de la curva de indiferencia. Por tanto en el punto óptimo, $(x_1^*, x_2^*) $, ha de cumplirse que ambas pendientes son iguales ¡Cuidado! Un error habitual al ver la siguiente ecuación es pensar que la $\mathrm{RMS}$ es el cociente de los precios. Esto no es así. Las curvas de indiferencia tienen en cada punto una pendiente (RMS) que depende de las preferencias, no de los precios. Lo que decimos es que en el punto óptimo, el valor de la RMS debe ser igual al cociente de precios. .

\[ \mathrm{RMS}(x_1^*, x_2^*) = -\frac{p_1}{p_2} \]

Como se ha visto en el ejemplo, el sistema tiene dos incógnitas a resolver $x_1$ y $x_2$, y unos parametros que son los precios y la renta. La solución que podemos obtener (siempre que tengamos una expresión concreta para la RMS) es el par de funciones de demanda individual de los dos bienes.

A continuación puedes ver dos ejemplos. No son cualitativamente distintos, pero el segundo requiere un poco más de operativa matemática.

Ejemplo

Ejemplo 

Resumiendo:

• Los razonamientos usados con datos concretos pueden aplicarse también a datos genéricos.
• Es importante distinguir en el problema qué variables son datos de valor no concretado, y qué variables son las incógnitas a resolver.
• Las funciones de demanda individual nos dan la cantidad óptima de cada bien (incógnitas) como funciones que dependen de precios y renta (parámetros). \[ x_1^* = x_1(p_1, p_2 , m) \quad \quad x_2^* = x_2(p_1, p_2 , m) \]
• En el caso de las preferencias bien comportadas (monótonas con curvas de indiferencia estrictamente convexas) el problema se resuelve con el sistema de ecuaciones formado por la recta presupuestaria y la condición de tangencia \[ \left. \begin{array}{c}p_1 \cdot x_1+ p_2 \cdot x_2=m \\ \\ \mathrm{RMS}(x_1, x_2) = -\frac{p_1}{p_2} \end{array} \right\} \]

Funciones de demanda individual
Parámetros   Incógnitas