La función de demanda de caramelos de Mary es $C(p_C, p_N, m)= \frac{m}{p_C + p_N}$.

Si Mary tiene una renta $m=120$ y el precio de las nubes es $p_N=4$, ¿cuál será la curva de demanda de caramelos?

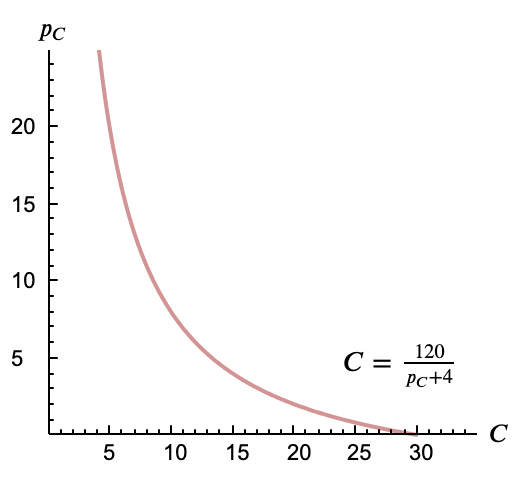
Usando los datos en la función de demanda la curva a representar es \[ C = \frac{120}{p_C + 4} \]

¿Cómo hacemos la representación?

Curiosamente esta tarea puede resultar más sencilla para quien use menos sus conocimientos de matemáticas. Basta con hacer una tabla con distintos precios y sus correspondientes cantidades de bien 1 según la función. Después representamos los ejes, usamos los valores de la tabla para situar los puntos correspondientes en la figura y los unimos con una línea (lo que hicimos en el ejemplo anterior).

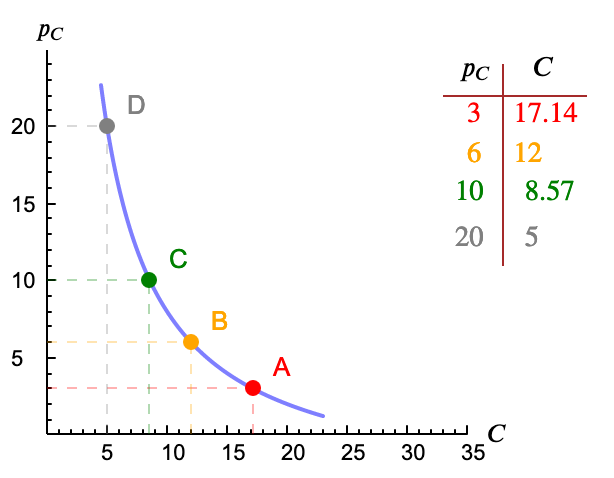
Quien sepa más mates dirá que simplemente dar valores es una mala estrategia a la hora de representar una función (a menos que se tenga claro de antemano qué tipo de función es) pues puede dar lugar a meteduras de pata imprevistas. Hay un 'procedimiento' estándar que busca detectar puntos especiales como cortes con los ejes, máximos y mínimos, concavidad y convexidad, posibles discontinuidades o comportamientos asintóticos. Y sólo después damos valores.

Pero además, al ver la función que vamos a representar hay una primera peculiaridad. Si la demanda de caramelos, $C$, depende del precio $p_C$, lo normal en matemáticas sería que $p_C$ estuviera en el eje horizontal y la variable dependiente, $C$, en el eje vertical.* El 'procedimiento' de representación de funciones trabaja con este supuesto. Por ejemplo al hablar de máximos o mínimos lo relacionamos con punto más alto o más bajo en la figura.

Si no nos permiten cambiar los ejes de posición porque "siempre se han puesto así" habrá que cambiar la función, despejando el precio en función de la cantidad:

\[ C = \frac{120}{p_C + 4} \quad \Longrightarrow \quad p_C = \frac{120 - 4 C}{C} \] Ahora sí podemos aplicar la rutina y decir que es una función con pendiente negativa, que corta el eje horizontal en $C=30$ y no está definida para $C=0$, pero su valor tiende a infinito si $C$ se acerca a 0. Es, por tanto, asintótica al eje vertical. También es estrictamente convexa.

Ahora que sabemos la forma que tiene sí daríamos algún valor para 'colocarla en su sitio'.