Un consumidor tiene una curva de demanda del bien x, \[ x= 100 - 2 \cdot p \]

El precio vigente es $p=25$

• ¿Comprará bien $x$? ¿Cuánto?Sol.
  Pregunta trivial (de calentamiento), puesto que tenemos la curva de demanda. \[ x(25) = 100 - 2 \cdot 25 = 50 \]
• ¿Cuánto dinero pagará? Sol.
  Si el precio es 25 y compra 50 unidades el pago total será $25 \times 50 = 1250$
• ¿Cuánto habría estado dispuesto a pagar como máximo por esas 50 unidades del bien?Sol.
  Nos están preguntando por el Excedente Bruto. Habrá que calcularlo..

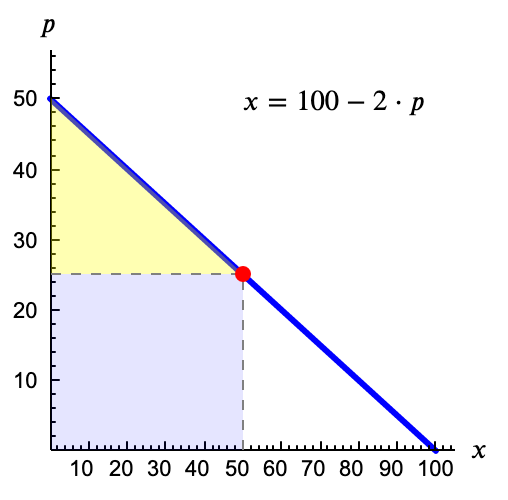
• Calcula el Excedente Bruto correspondiente a $x=50$. Sol.
  Es el área bajo la curva de demanda (coloreada en la figura). Dado que la demanda es recta, podemos calcularla como suma del triángulo y el rectángulo: \[ \frac{50 \cdot (50-25)}{2} + 50 \cdot 25 = 1875 \]
• ¿Qué ha ganado el consumidor al ir al mercado? Sol.
  Según hemos calculado estaba dispuesto a pagar 1875 por las 50 unidades, pero el mercado sólo le ha pedido 1250. Desde su punto de vista ha ganado $1875-1250 = 625$ con ese intercambio.
• Y si él ha ganado, ¿quién ha perdido?Sol.
  No siempre alguien tiene que perder para que otro pueda ganar. Dado que hablamos de valoraciones subjetivas, es posible que el vendedor valorara las 50 unidades en menos de 1250, y él también considere que ha salido ganando con el intercambio.