Las preferencias cuasilineales son aquellas que pueden ser representadas mediante funciones de utilidad que dependen linealmente de uno de los bienes y no linealmente del otro.*
La siguiente función depende linealmente de $x_2$. Normalmente, por simplicidad en las interpretaciones, trabajaremos con estas formas funcionales.
Pero situar los bienes en uno u otro eje es una decisión arbitraria. Igualmente, una función cuasilineal sería
\[ \mathrm{U}(x_1, x_2) = a x_1 + f(x_2) \]
Una peculiaridad de las preferencias con esta forma funcional es que la relación marginal de sustitución sólo depende de la cantidad de $x_1$; las curvas de indiferencia se desplazan verticalmente
En el caso de preferencias cuasilineales con la forma funcional $ \mathrm{U}(x_1, x_2) = a x_1 + f(x_2) $, las curvas de indiferencia se desplazan horizontalmente; la relación marginal de sustitución sólo depende de la cantidad de $x_2$.
Ejemplo
.
Ejemplo
En la figura, el mapa de indiferencia para unas preferencias cuasilinares se muestra junto con la RMS de las curvas de indiferencia en $x_1=25$ (en la línea discontinua).
La pendiente de la curva de indiferencia (RMS) para una determinada $x_1$ es la misma en cada curva: Las curvas de indiferencia se desplazan verticalmente.
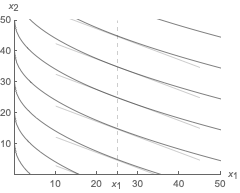
El consumidor de la figura tiene preferencias cuasilineales representadas por la función de utilidad \[ \mathrm{U}(x_1, x_2) = 5 \sqrt{x_1} + x_2\]
La relación marginal de sustitución es
\[ \mathrm{RMS}(x_1, x_2) = -\frac{5}{2\sqrt{x_1}}\]Para un determinado $x_1$, digamos 25, obtenemos $\mathrm{RMS}(25, x_2) = -\frac{1}{2}$.
En la figura, el mapa de indiferencia para una preferencia cuasiliniar se muestra junto con la RMS de las curvas de indiferencia en $x_2=25$ (en la línea discontinua).
La pendiente de la curva de indiferencia (RMS) para una determinada $x_2$ es la misma en cada curva: Las curvas de indiferencia se desplazan horizontalmente.
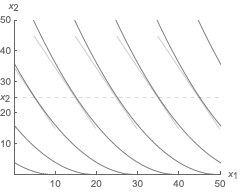
El consumidor de la figura tiene preferencias cuasilineales representadas por la función de utilidad: \[ \mathrm{U}(x_1, x_2) = x_1+ 5 \sqrt{x_2}\]
La relación marginal de sustitución es
\[ \mathrm{RMS}(x_1, x_2) = -\frac{1}{\frac{5}{2\sqrt{x_2}}}=-\frac{2\sqrt{x_2}}{5}\]Para un determinado $x_2$, digamos 25, obtenemos $\mathrm{RMS}(x_1, 25) = -2$.