(Concepto matemático)$\quad \quad$
Una curva de nivel (contorno) de una función de dos variables es una curva que une todos los puntos con el mismo valor de la función. Para cada valor de la función, la intersección de un plano horizontal con la gráfica tridimensional a esa altura corresponde a una curva de nivel.
Ejemplo
Para la función de utilidad $U(x_1,x_2)=\sqrt{x_1\cdot x_2}$, la figura muestra el contorno correspondiente al punto $A=(9,4)$ cuyo nivel de utilidad es 6.
A la derecha podemos ver el gráfico tridimensional de la función, en el que el punto A y su contorno están dibujados en rojo. A la izquierda la correspondiente curva de nivel 6 es la curva gruesa.

El contorno de valor 6 está formado por todas las cestas con utilidad 6 (la curva de indiferencia de nivel 6); $6=\sqrt{x_1 x_2}$.
Despejando $x_2$ (la variable representada en el eje vertical), la ecuación queda $x_2=\frac{36}{x_1}$
Un mapa de nivel es un gráfico de dos dimensiones que muestra algunas curvas de nivel (en general, a alturas equidistantes) del gráfico de tres dimensiones proyectado en el plano a altura 0. Cada curva de nivel corresponde a un valor de la función que puede indicarse con una etiqueta.
Ejemplo
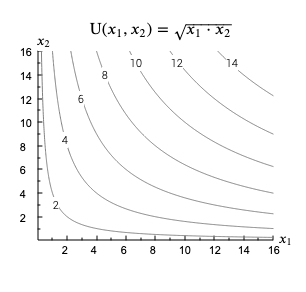
Para la función de utilidad $U(x_1, x_2)=\sqrt{x_1 x_2}$, la figura muestra un mapa de nivel compuesto por las curvas de nivel 2, 4, 6, 8, 12 y 14.