Elige la opción que creas correcta y clica el botón 'Comprobar respuesta'.
Incluso si aciertas con tu elección, puede ser interesante elegir las opciones entre las que has dudado para ver explicaciones adicionales.
La renta del consumidor es $m=120$ y los precios de los bienes son $p_1=3$ y $p_2=4$.
¡Vuelve a intentarlo!
Cada unidad de bien 1 cuesta su precio, $p_1=3$. Por lo tanto, con una renta de 120 puedes comprar $\frac{m}{p_1}=\frac{120}{3}=40$ unidades a lo sumo.
¡Vuelve a intentarlo!
No se la puede permitir puesto que necesitaría una renta de $3*15+4*20=125$.
Vuelve a intentarlo!
El consumidor puede comprar o bien un máximo de 40 unidades de bien 1 o bien un máximo de 30 unidades de bien 2, pero no puede comprar a la vez 40 unidades de bien 1 y 30 de bien 2.
✅ Bien hecho !!
Puede comprarla, aunque no se gastaría toda su renta. Sólo cuesta $3*20+4*10=100$.La renta del consumidor es $m=120$ y los precios de los bienes son $p_1=2$ y $p_2=4$. Obtén la ecuación de la recta presupuestaria y represéntala gráficamente. Basándote en tu gráfico, selecciona la opción correcta.
¡Vuelve a intentarlo!
El eje horizontal indica la cantidad de bien 1, por tanto la recta presupuestaria corta el eje horizontal en $\frac{120}{2}=60$ (la máxima cantidad de bien 1 que se puede comprar con la renta).
¡Vuelve a intentarlo!
Representamos el bien 2 en el eje vertical, por tanto el punto de corte será la máxima cantidad de bien 2 que puede comprarse con la renta, $\frac{120}{4}=30$.
✅ Genial !!
La pendiente de la recta presupuestaria es la tangente del ángulo que forma con el eje horizontal, $\frac{30}{60}$ (la recta presupuestaria junto con los ejes forman un triángulo rectángulo; la tangente de este ángulo será el cociente entre el cateto opuesto y el contiguo: $\frac{30}{60}=\frac{1}{2}$).
¡Vuelve a intentarlo!
La pendiente de la recta presupuestaria es la tangente del ángulo que forma con el eje horizontal.La recta presupuestaria junto con los ejes forman un triángulo rectángulo; la tangente de ese ángulo será el cociente entre el cateto opuesto y el contiguo.
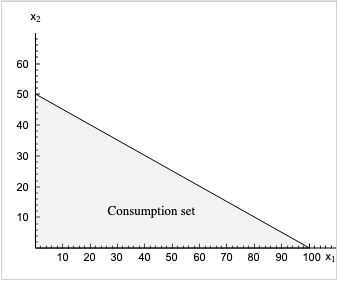
El conjunto presupuestario de un consumidor está representado en la siguiente figura. Selecciona la opción consistente con la figura.
Vuelve a intentarlo!
El eje horizontal indica la cantidad de bien 1. La recta presupuestaria lo corta en 100 lo cual indica la cantidad máxima de bien 1 que puede adquirir con la renta. (50 es la máxima cantidad que se puede comprar de bien 2 con la renta).
¡Vuelve a intentarlo!
El consumidor puede comprar 100 unidades de bien 1, pero entonces no queda renta para comprar bien 2; cesta (100,0) es el punto de corte con el eje horizontal. De manera similar el consumidor puede comprar 50 unidades de bien 2 gastándose toda la renta, y no comprando nada de bien 1.
¡Vuelve a intentarlo!
Puedes comprar el doble de bien 1 que de bien 2 precisamente porque vale la mitad. Hemos visto en la teoría que la pendiente de la recta presupuestaria es ($\frac{\Delta x_2}{\Delta x_1}=\frac{50}{100}=\frac{1}{2}$) que es el cociente de precios $-\frac{p_1}{p_2}=-\frac{1}{2}$.
✅ Eso es !!
Sabemos que la recta presupuestaria corta el eje vertical en 50, lo que significa que $\frac{m}{p_2}=50$. Reordenando tenemos $p_2=\frac{m}{50}$. De la misma manera podemos obtener $p_1=\frac{m}{100}$. Por ejemplo, si $m=1000$ sabemos que los precios son $p_1=10$ y $p_2=20$.Sabemos que un consumidor gasta toda su renta en la cesta $(20,60)$. También se gastaría todo su dinero con la cesta $(25,50)$.
¡Vuelve a intentarlo!
El precio es el mismo para todas las unidades de un bien, por lo que la tasa de sustitución entre bienes a precios de mercado es constante. De acuerdo al enunciado, la tasa de sustitución en el mercado es de uno por dos.
¡Vuelve a intentarlo!
Según el enunciado, la tasa de sustitución entre bienes es de uno a dos. Por tanto, partiendo de $(25,50)$, para aumentar el bien 1 en 15 unidades, el bien 2 tiene que reducirse al menos en 30: cesta (40,20).
¡Vuelve a intentarlo!
Es cierto que Para consumir 5 unidades adicionales de bien 1 el conumidor tiene que renunciar a 10 de bien 2. Pero entonces, la pendiente de la recta presupuestaria es $\frac{\Delta x_2}{\Delta x_1}=\frac{-10}{5}=-\frac{p_1}{p_2}$.
✅ Perfecto !!
Los precios son los mismos para todas las unidades, por tanto la tasa de sustitución entre bienes a precios de mercado es constante. Esta tasa de sustitución coincide con la tasa de sustitución de $(20,60)$ a $(25,50)$.